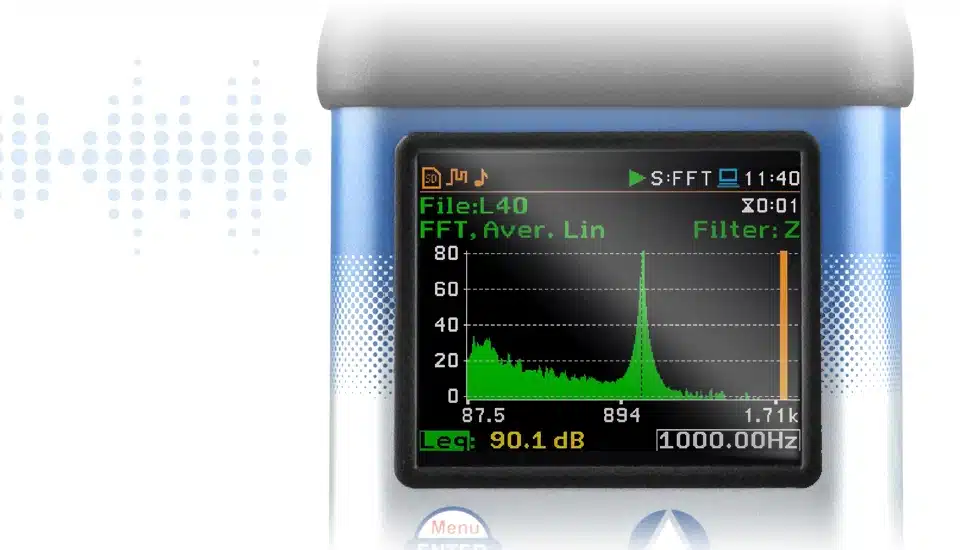
FFT Szybka Transformata Fouriera
FFT Szybka Transformata Fouriera umożliwia rozkład sygnałów na ich sinusoidy składowe, umożliwiając analizę w dziedzinie częstotliwości.
FFT Szybka Transformata Fouriera umożliwia rozkład sygnałów na ich sinusoidy składowe, umożliwiając analizę w dziedzinie częstotliwości.
Szybka transformata Fouriera (FFT) to algorytm używany do obliczania dyskretnej transformaty Fouriera (DFT) i jej odwrotności. DFT jest przekształceniem stosowanym w przetwarzaniu sygnałów i przetwarzaniu obrazu, wśród wielu innych obszarów, w celu przekształcenia dyskretnego sygnału w jego reprezentację w dziedzinie częstotliwości. FFT przyspiesza proces obliczania DFT, umożliwiając jego wykorzystanie w aplikacjach czasu rzeczywistego i dla dużych zbiorów danych.
Analiza FFT została opracowana przez Jamesa W. Cooleya i Johna W. Tukeya w 1965 roku. Ich wersja algorytmu znacznie zmniejszyła złożoność obliczeniową przetwarzania dużych zbiorów danych, czyniąc cyfrowe przetwarzanie sygnałów bardziej wykonalnym i wydajnym.
FFT to zoptymalizowany algorytm przeznaczony do szybkiego obliczania dyskretnej transformaty Fouriera (DFT) i jej odwrotności. Zaletą FFT jest jego wydajność. Podczas gdy bezpośrednie obliczenie DFT wymaga O(N^2) operacji (czas kwadratowy), algorytm FFT umożliwia wykonanie tego samego obliczenia w O(N log N) operacjach, co stanowi znaczne przyspieszenie dla dużych zbiorów danych.
Szybka transformata Fouriera (FFT) to algorytm, który szybko oblicza dyskretną transformatę Fouriera (DFT) i jej odwrotność. FFT jest używana w szerokim zakresie zastosowań, głównie dlatego, że może konwertować sygnał z dziedziny czasu na dziedzinę częstotliwości i odwrotnie. Zrozumienie składowych częstotliwościowych sygnału może zapewnić cenny wgląd w naturę, zachowanie i właściwości tego sygnału.
Co to jest równanie FFT?
FFT jest algorytmem, który efektywnie oblicza DFT, więc równanie jest takie samo jak równanie DFT. Warto jednak zauważyć, że istnieje wiele różnych algorytmów FFT (np. radix-2, split-radix itp.), a każdy z nich ma swoje własne kroki i zawiłości.
Co to jest DFT?
DFT to potężne narzędzie matematyczne służące do przekształcania dyskretnych, okresowych sygnałów z ich reprezentacji w dziedzinie czasu na reprezentację w dziedzinie częstotliwości. Pozwala to na analizę i manipulację w dziedzinie częstotliwości przed potencjalnym przekształceniem z powrotem do dziedziny czasu za pomocą odwrotnej DFT.
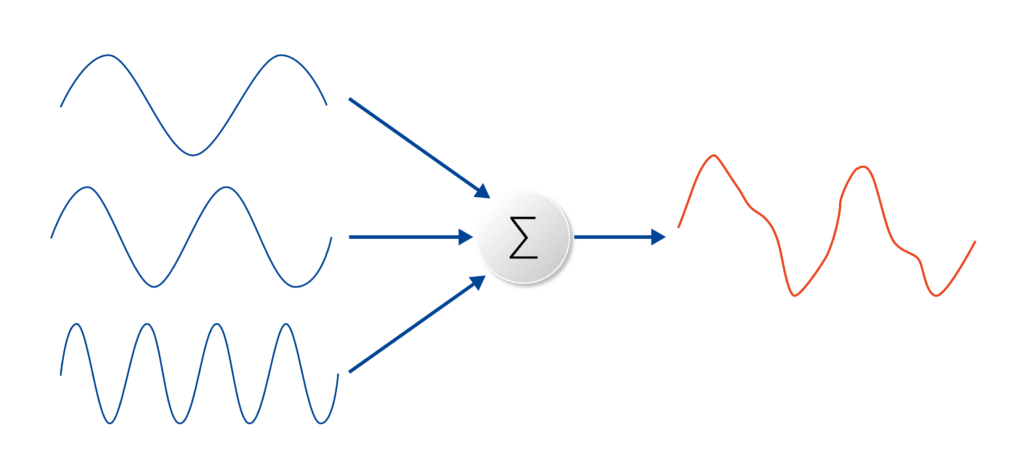
DFT, którą wydajnie oblicza FFT, jest zdefiniowana dla sekwencji x[n] o długości N jako:
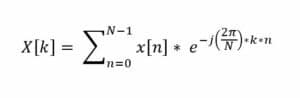
Gdzie:
e jest podstawą logarytmu naturalnego (w przybliżeniu równą 2,71828).
Istnieje wiele zastosowań FFT:
Zalety stosowania FFT to:
Różnica między szybką transformacją Fouriera (FFT) a transformacją Fouriera (FT) leży w sposobie obliczeń i efektywności. FFT to specjalna, wydajniejsza metoda obliczania dyskretnej transformaty Fouriera (DFT), która jest z kolei dyskretnym odpowiednikiem ciągłej transformaty Fouriera (FT).
FT przekształca sygnał ciągły w dziedzinie czasu na sygnał ciągły w dziedzinie częstotliwości. W praktyce jednak często mamy do czynienia z sygnałami próbkowanymi (dyskretnymi), dlatego używa się DFT, która przekształca ciąg próbek sygnału w ciąg równie licznych próbek jego widma częstotliwościowego.
FFT to zoptymalizowana wersja DFT, która redukuje złożoność obliczeniową z O(N^2) do O(N log N), gdzie N to liczba próbek. Dzięki temu FFT jest znacznie szybsza w obliczeniach niż bezpośrednie zastosowanie DFT, szczególnie dla dużych zestawów danych. Optymalizacje te opierają się na dekompozycji DFT na mniejsze DFT o rozmiarach będących potęgami liczby 2, co sprawia, że FFT jest niezwykle ważna w cyfrowym przetwarzaniu sygnałów.
Transformata Fouriera rozkłada przebieg na sumę sinusoid o różnych częstotliwościach. Oznacza to, że transformata Fouriera reprezentuje te same informacje, co oryginalny kształt fali, tylko w dziedzinie częstotliwości (w przeciwieństwie do dziedziny czasu). Metodologia analizy transformaty Fouriera jest niezbędna do skutecznego rozwiązywania problemów w wielu kontekstach inżynieryjnych i naukowych. Wizualnie, transformata Fouriera jest reprezentowana przez wykres wskazujący amplitudę i częstotliwość każdej sinusoidy.
Poniższe równanie przedstawia ciągłą transformatę Fouriera i pokazuje, w jaki sposób dowolny sygnał czasu ciągłego może być reprezentowany jako suma (całka) sinusoid o wszystkich możliwych częstotliwościach:
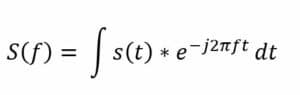
Gdzie:
Szybka transformata Fouriera (FFT) może być wykonywana zarówno w czasie rzeczywistym, jak i w kontekście przetwarzania końcowego. Rozróżnienie między nimi zależy przede wszystkim od zastosowania i specyficznych wymagań danego zadania.
Pomiar FFT (Fast Fourier Transform) polega na przechwyceniu sygnału w dziedzinie czasu, a następnie przekształceniu go w dziedzinę częstotliwości w celu analizy jego składowych częstotliwościowych. Oto podstawowy przewodnik krok po kroku dotyczący pomiaru FFT:
Do pomiaru FFT można użyć różnych urządzeń i narzędzi:
Analizator FFT, czyli analizator szybkiej transformaty Fouriera, to urządzenie zapewniające analizę częstotliwościową sygnałów, powszechnie stosowane w audio, badaniach wibracji i różnych innych zastosowaniach. Wykorzystuje on algorytm FFT do przekształcania sygnału z jego oryginalnej domeny czasowej w domenę częstotliwości. Oto bardziej szczegółowy opis działania analizatora FFT:
Wyciek widmowy to zjawisko, które może zniekształcać wyniki analizy FFT. Podczas wykonywania FFT istnieje nieodłączne założenie, że sygnał w rekordzie czasu powtarza się w nieskończoność. Założenie to jest jednak naruszane, jeśli liczba cykli sygnału w tym zapisie nie jest liczbą całkowitą (niecałkowitą). Ta rozbieżność między zakładaną powtarzalnością a rzeczywistym sygnałem może prowadzić do wycieku widmowego. Wyciek widmowy może rozmyć energię z określonej częstotliwości w sąsiednich liniach lub przedziałach częstotliwości, czyniąc wynik mniej dokładnym.
Zarówno antyaliasing, jak i częstotliwość Nyquista są kluczowymi pojęciami, które należy zrozumieć podczas próbkowania sygnałów i wykonywania analiz FFT:
Podczas próbkowania sygnału ciągłego w celu uzyskania sygnału dyskretnego do przetwarzania cyfrowego (takiego jak FFT), twierdzenie Nyquista (lub twierdzenie Shannona-Nyquista dotyczące próbkowania) stwierdza, że częstotliwość próbkowania musi być co najmniej dwa razy większa od najwyższej częstotliwości występującej w sygnale, aby móc w pełni reprezentować i później zrekonstruować oryginalny sygnał ciągły bez utraty informacji. Najwyższa dopuszczalna częstotliwość w sygnale, która stanowi połowę częstotliwości próbkowania, to częstotliwość Nyquista. Matematycznie, jeśli fS jest częstotliwością próbkowania, częstotliwość Nyquista fN wynosi: fN=fS/2
Aby zapobiec aliasingowi, stosowany jest filtr antyaliasingowy. Podczas wykonywania FFT na próbkowanych danych, jeśli dane nie zostały poprawnie spróbkowane (tj. z wystarczająco dużą częstotliwością) lub jeśli nie zastosowano odpowiedniego filtra antyaliasingowego, wynikowe widmo częstotliwości może zawierać częstotliwości aliasingowe. Może to prowadzić do błędnych lub mylących interpretacji zawartości częstotliwościowej sygnału.
Filtr antyaliasingowy jest analogowym filtrem dolnoprzepustowym stosowanym do sygnału przed próbkowaniem. Jego celem jest tłumienie lub eliminowanie częstotliwości w sygnale, które są wyższe niż częstotliwość Nyquista, zapewniając w ten sposób, że próbkowana wersja sygnału nie zawiera mylących informacji o częstotliwości. W ten sposób zapewnia, że dyskretna wersja sygnału jest prawdziwą reprezentacją sygnału ciągłego do częstotliwości Nyquista.
Uśrednianie w kontekście FFT służy do poprawy stosunku sygnału do szumu i zapewnienia dokładniejszej reprezentacji widma, zwłaszcza podczas analizy sygnałów nieokresowych, takich jak szum lub muzyka.
FFT Audio jest odnosi się do procesu konwersji sygnału audio z domeny czasu do domeny częstotliwości. Ta transformacja pozwala nam zobaczyć różne składowe częstotliwości (basy, średnie, wysokie tony itp.) obecne w sygnale audio w danym momencie. Na przykład, podczas analizy utworu muzycznego, FFT rozbije sygnał, aby pokazać, ile energii występuje na każdej częstotliwości. Może to ujawnić dudnienie bębna basowego o niskiej częstotliwości, tony średnie gitary i skwierczenie talerza o wysokiej częstotliwości w tym samym czasie.
Analizator Audio FFT to narzędzie lub urządzenie, które stosuje FFT do sygnałów audio, umożliwiając użytkownikom wizualizację zawartości częstotliwościowej sygnału. Wizualizacja ta ma często postać widma, w którym oś x reprezentuje częstotliwość (od niskiej do wysokiej), a oś y reprezentuje amplitudę (często w skali logarytmicznej, takiej jak dB). Analizatory audio FFT są wykorzystywane w wielu zastosowaniach:
Ludzki zakres słyszalności jest ogólnie uważany za zakres od 20 Hz do 20 000 Hz (lub 20 kHz). Tak więc, gdy analizator audio FFT jest używany do analizy sygnałów audio przeznaczonych do spożycia przez ludzi (takich jak muzyka lub mowa), widmo częstotliwości zazwyczaj koncentruje się na tym zakresie. Warto zauważyć, że chociaż słyszymy w tym zakresie, nasza wrażliwość na częstotliwości nie jest jednolita. Ludzie są najbardziej wrażliwi na częstotliwości dźwięku od 2 kHz do 4 kHz i mniej wrażliwi na bardzo niskie i bardzo wysokie częstotliwości.
Wykorzystanie okien ma kluczowe znaczenie podczas wykonywania pomiarów opartych na FFT. Okna pomagają w łagodzeniu pewnych kwestii związanych z naturą FFT i właściwościami analizowanych sygnałów. Funkcja okienkowania to funkcja matematyczna, która jest stosowana do sygnału w celu złagodzenia skutków wycieku widmowego. Różne okna mają różne właściwości, a wybór okna wpływa na wynik analizy FFT. Często stosowane przykłady okien to Hanning lub Flat Top. Hanning (lub Hann) jest to powszechnie stosowane okno, które jest rodzajem okna kosinusowego. Pomaga zmniejszyć wyciek widmowy. Flat Top zapewnia bardzo precyzyjne pomiary amplitudy, ale mniej dokładne pod względem rozdzielczości częstotliwości. Okno prostokątne, w którym nie jest stosowana żadna funkcja okienkowania nazywane jest jednolite (uniform).
FFT w przyrządach Svantek umożliwia użytkownikom zrozumienie składowych częstotliwości dźwięków lub wibracji, które mierzą. Ma to kluczowe znaczenie dla różnych zastosowań, w tym oceny hałasu i wibracji, rozwiązywania problemów i nie tylko. W przyrządach Svantek, FFT (Szybka Transformata Fouriera) jest algorytmem obliczeniowym, który przekształca sygnał z jego oryginalnej domeny (domena czasu) w jego składowe częstotliwości. Zapewnia on środki do analizy różnych składowych częstotliwości sygnałów, ułatwiając szczegółowy wgląd w charakterystykę pomiarów dźwięku lub wibracji. Funkcja FFT w przyrządach Svantek działa w połączeniu z miernikiem poziomu i może wyświetlać wyniki jako widma w dedykowanym widoku widma.
Zastosowania analizatorów FFT Svantek obejmują zarówno analizę akustyczną, jak i analizę drgań, od badań hałasu środowiskowego po monitorowanie maszyn przemysłowych:
Metoda FFT w drganiach budynków jest opisana w niemieckiej normie DIN 4150-3. Metoda ta wymaga przeprowadzenia analizy FFT dla szczytowej prędkości cząstek (PPV), w taki sposób, że środek okna FFT jest umieszczony dokładnie na PPV. Wynikiem takiej analizy jest wartość PPV i odpowiadająca jej częstotliwość dominująca (DF) dla każdej osi (X,Y,Z). Każda para PPV i jej DF są używane jako współrzędne punktu, które są porównywane z krzywą graniczną.
FFT Szybka Transformata Fouriera : Kluczowe wnioski:
Autoryzowany konsultant SVANTEK pomoże Ci w szczegółach, takich jak wymagane akcesoria do monitorowania hałasu i wibracji.
