O que é a Transformada Rápida de Fourier FFT?
A Transformada Rápida de Fourier FFT é um algoritmo usado para calcular a transformada discreta de Fourier (DFT) e sua inversa de forma mais eficiente. A DFT é uma transformada utilizada no processamento de sinais e processamento de imagens, entre muitas outras áreas, para transformar um sinal discreto em sua representação no domínio da frequência. A FFT acelera o processo de computação da DFT, permitindo que ela seja utilizada em aplicações em tempo real e para grandes conjuntos de dados.
Quem inventou a FFT?
A FFT foi co-descoberta por James W. Cooley e John W. Tukey em 1965. Embora o algoritmo tenha sido certamente um avanço, deve-se notar que muitas de suas ideias fundamentais já existiam há algum tempo, mas o trabalho de Cooley e Tukey trouxe ganhou destaque na era digital, especialmente com a ascensão da computação digital. Sua versão do algoritmo reduziu bastante a complexidade computacional do processamento de grandes conjuntos de dados, tornando o processamento de sinais digitais mais viável e eficiente.
O FFT é um algoritmo otimizado projetado para calcular rapidamente a Transformada Discreta de Fourier (DFT) e sua inversa. A vantagem da FFT reside na sua eficiência. Embora um cálculo direto da DFT exija operações O(N^2) (tempo quadrático), o algoritmo FFT permite o mesmo cálculo em operações O(N log N), o que é uma aceleração significativa para grandes conjuntos de dados.
O algoritmo FFT (Fast Fourier Transform) é usado em uma ampla gama de aplicações porque pode converter um sinal de seu domínio de tempo para seu domínio de frequência e vice-versa. Compreender os componentes de frequência de um sinal pode fornecer informações valiosas sobre a natureza, o comportamento e as propriedades desse sinal.
Qual é a equação FFT?
A FFT é um algoritmo que calcula eficientemente a DFT, portanto a equação é igual à equação da DFT. No entanto, é importante notar que existem muitos algoritmos FFT diferentes (por exemplo, radix-2, split-radix, etc.), e cada um tem suas próprias etapas e complexidades específicas.
O que é o DFT?
A Transformada Discreta de Fourier DFT é uma ferramenta matemática poderosa usada para transformar sinais discretos e periódicos de sua representação no domínio do tempo em uma representação no domínio da frequência. Isso permite a análise e manipulação no domínio da frequência antes de potencialmente transformar de volta para o domínio do tempo com a DFT inversa. A DFT, que a FFT calcula eficientemente, é definida para uma sequência x[n] de comprimento N como:
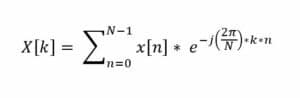
Where:
- X[k] is the k-th element of the frequency-domain representation.
- x[n] is the n-th element of the time-domain signal.
e is the base of the natural logarithm (approximately equal to 2.71828).
- j is the imaginary unit (satisfying j2=−1).

O que são aplicativos FFT?
Existem muitas aplicações FFT:
- Mecânica Aplicada (por exemplo, dinâmica estrutural, supressão de vibração de asas de aeronaves, diagnóstico de dinâmica de máquinas, modelagem de usinas nucleares, análise de vibração)
- Som e acústica (por exemplo, imagem acústica, sonar passivo, transdutores ultrassônicos, processamento de matriz, medição acústica de arquitetura, síntese musical)
- Engenharia Biomédica (por exemplo, diagnóstico de obstrução das vias aéreas, monitoramento de fadiga muscular, avaliação de danos nas válvulas cardíacas, caracterização da estrutura tecidual, investigação de distúrbios gástricos, diagnóstico de pacientes cardíacos, compressão de dados de EEG, investigação de dinâmica arterial)
- Métodos Numéricos (por exemplo, interpolação de alta velocidade, método de gradiente conjugado, problemas de valor limite, equações de Riccati e Dirichlet, integral de Rayleigh, equação integral de Wiener-Hopf, equação de difusão, integração numérica, transformada de Karhunen-Loeve, equações diferenciais elípticas)
- Processamento de sinal (por exemplo, filtros combinados, deconvolução, análise espectral em tempo real, análise Cepstrum, estimativa da função de coerência, síntese e reconhecimento de fala, geração de processo aleatório, estimativa da função de transferência, remoção de eco/reverberação)
- Instrumentação (por exemplo, cromatografia, microscopia, espectroscopia, difração de raios X, eletrocardiografia)
- Radar (medição de seção transversal, indicador de alvo móvel, abertura sintética, processador Doppler, compressão de pulso, rejeição de interferência)
- Eletromagnetismo (propagação de linha de microfita, espalhamento de corpos condutores, padrões de radiação de antena, capacitância de substrato dielétrico, análise de antena phased-array, reflectometria no domínio do tempo, análise de guia de onda, análise de rede)
- Comunicações (Análise de sistemas, Transmultiplexadores, Demoduladores, Sistema scrambler de fala, Filtragem multicanal, Sinalização M-ária, Detecção de sinal, Filtros digitais de alta velocidade, Sistemas de codificação de voz, Compressão de largura de banda de vídeo)
- Diversos (por exemplo, magnetômetros, metalurgia, sistemas de energia elétrica, restauração de imagens, análise de sistemas não lineares, geofísica, resposta transitória GaAs FET, modelagem de circuitos integrados, controle de qualidade)
Quais são os benefícios de usar FFT?
Há muitos benefícios em usar FFT em várias aplicações:
- Análise de Sinal: Ao converter um sinal no domínio do tempo em seus componentes de frequência, os usuários podem identificar as frequências dominantes presentes em um sinal, detectar qualquer ruído indesejado ou analisar harmônicos.
- Redução de ruído: No processamento de áudio ou imagem, frequências indesejadas (ruído) podem ser identificadas e removidas manipulando os componentes de frequência e convertendo o sinal de volta para o domínio do tempo.
- Compressão: No processamento digital de sinais, a representação de frequência de um sinal pode às vezes ser comprimida preservando apenas as frequências mais significativas, o que pode ser especialmente útil em técnicas de compressão de imagem e áudio.
- Projeto e implementação de filtros: Os filtros podem ser projetados e implementados de forma mais eficiente no domínio da frequência. Ao converter um sinal em sua representação de frequência, certos componentes de frequência podem ser amplificados, atenuados ou eliminados e depois transformados de volta no domínio do tempo.
- Convolução: A convolução no domínio do tempo é a multiplicação no domínio da frequência. Calcular a convolução usando FFT (convertendo para o domínio da frequência, multiplicando e depois convertendo novamente) pode ser mais rápido do que a convolução direta no domínio do tempo para sinais longos.
- Análise Espectral: Em campos como astronomia, geologia e oceanografia, a análise dos componentes de frequência dos sinais pode fornecer insights sobre fenômenos físicos.
- Análise Estrutural: Na engenharia civil, a FFT pode ser usada para analisar a resposta vibracional de estruturas, ajudando os engenheiros a detectar frequências ressonantes que podem ser prejudiciais à estrutura.
- Telecomunicações: A FFT é usada na modulação de sinais para transmissão e na demodulação deles após o recebimento.
- Processamento de áudio: FFT ajuda na equalização, reverberação, correção de tom e muitos outros efeitos de áudio, analisando e manipulando sinais no domínio da frequência.
- Imagens Médicas: Na ressonância magnética (ressonância magnética), a FFT é usada para transformar os sinais recebidos do corpo em imagens.
Qual é a diferença entre FFT e Transformada de Fourier?
A Transformada de Fourier é um conceito matemático mais amplo usado para transformar sinais entre os domínios do tempo (ou espacial) e da frequência. A Transformada Rápida de Fourier é um algoritmo específico e otimizado para calcular o DFT, que é a versão amostrada do FT, de maneira mais rápida.
Como funciona a Transformada de Fourier?
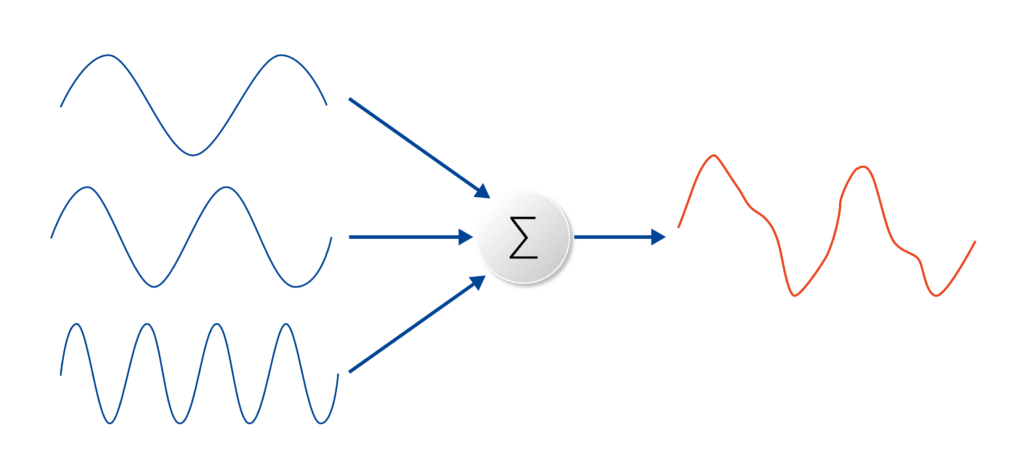
A transformada de Fourier decompõe uma forma de onda em uma soma de senoides de diferentes frequências. Isto significa que a transformada de Fourier representa a mesma informação que a forma de onda original, apenas no domínio da frequência (em oposição ao domínio do tempo). A metodologia de análise da transformada de Fourier é essencial para a resolução eficaz de problemas em muitos contextos científicos e de engenharia. Visualmente, a transformada de Fourier é representada por um diagrama que indica a amplitude e a frequência de cada senóide. A equação abaixo representa a transformada de Fourier em tempo contínuo. A equação captura como qualquer sinal de tempo contínuo pode ser representado como uma soma (integral) de senoides de todas as frequências possíveis:
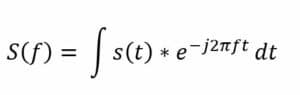
Onde:
- S(f) representa a transformada de Fourier de s(t).
- e é a base do logaritmo natural.
- j é a unidade imaginária (com j2=−1).
A FFT é feita em tempo real ou é pós-processada?
A Transformada Rápida de Fourier (FFT) pode ser aplicada em contextos de tempo real e pós-processamento. A distinção entre os dois depende principalmente da aplicação e dos requisitos específicos da tarefa em questão.
FFT em tempo real:
- Aplicações: A FFT em tempo real é usada em aplicações onde são necessárias informações imediatas no domínio da frequência. Os exemplos incluem analisadores de espectro em tempo real, processamento de efeitos de áudio (como equalizadores em tempo real), certas aplicações de telecomunicações e controle ativo de ruído.
- Desafios: A execução de FFT em tempo real requer hardware rápido e algoritmos otimizados, especialmente quando a taxa de dados é alta ou o tamanho da FFT é grande. A latência pode ser um fator crítico em aplicações de tempo real, portanto o sistema deve ser projetado para lidar com os dados dentro das restrições de tempo.
- Benefícios: O processamento em tempo real pode fornecer feedback imediato, o que é essencial em certas aplicações como processamento de áudio, sistemas de monitoramento ao vivo ou sistemas de controle ativo.
Pós-processamento FFT:
- Aplicações: O pós-processamento normalmente é empregado quando não há necessidade imediata dos dados transformados ou quando são necessárias análises mais complexas e computacionalmente intensivas. Os exemplos incluem análise de vibração de máquinas (onde os dados são coletados ao longo do tempo e depois analisados), estudos de pesquisa e certas tarefas de processamento de imagens.
- Desafios: Embora possa não haver as mesmas restrições de tempo que no processamento em tempo real, o pós-processamento pode envolver o tratamento de grandes conjuntos de dados, exigindo mecanismos eficientes de armazenamento e recuperação.
- Benefícios: Sem restrição de tempo, uma análise mais detalhada ou abrangente pode ser feita. Os dados podem ser reanalisados com diferentes parâmetros, algoritmos ou modelos, conforme necessário.
Como medir a FFT?
Medir a FFT (Fast Fourier Transform) envolve capturar um sinal no domínio do tempo e depois transformá-lo no domínio da frequência para analisar seus componentes de frequência. Aqui está um guia passo a passo básico sobre como medir a FFT:
- Aquisição de sinal:
- Sinal de entrada: Certifique-se de que o sinal de interesse, seja de um microfone, sensor de vibração ou qualquer outra fonte, esteja acessível para medição.
- Amostragem: Amostra digital do sinal usando um Conversor Analógico para Digital (ADC). A taxa de amostragem deve ser pelo menos duas vezes o componente de frequência mais alta do sinal (de acordo com o teorema de Nyquist) para evitar aliasing.
- Janelas (opcional, mas recomendada):
- Antes de aplicar a FFT, geralmente é uma boa ideia aplicar uma função de janela ao sinal no domínio do tempo. Isto pode minimizar o vazamento espectral, que pode ocorrer devido ao comprimento finito do sinal amostrado. Funções de janela comuns incluem Hanning, Hamming, Blackman e Kaiser.
- Aplique o algoritmo FFT:
- Usando hardware dedicado (como um processador de sinal digital) ou software (como MATLAB, a biblioteca numpy do Python ou outras bibliotecas FFT), transforme o sinal janelado no domínio do tempo no domínio da frequência.
- Analise o resultado:
- A saída da FFT será uma matriz complexa, com informações de magnitude e fase. Para muitas aplicações, apenas a magnitude é de interesse.
- O espectro de magnitude mostrará a amplitude dos componentes de frequência do sinal.
- Você pode determinar as frequências dominantes no sinal identificando picos no espectro de magnitude.
- Resolução e tamanho:
- A resolução de frequência da FFT é determinada pela taxa de amostragem dividida pelo número de pontos na FFT. Por exemplo, se você amostrasse um sinal de 1kHz e usasse uma FFT de 1.000 pontos, sua resolução de frequência seria de 1Hz.
- Usar um tamanho de FFT maior proporcionará melhor resolução de frequência, mas exigirá mais cálculos.
- FFT inversa (IFFT):
- Se necessário, você pode transformar os dados no domínio da frequência de volta para o domínio do tempo usando a Transformada Rápida Inversa de Fourier (IFFT).
- Visualização:
- Exibir o espectro de frequência usando software ou hardware de exibição dedicado. A visualização auxilia na compreensão dos componentes de frequência e suas respectivas amplitudes.
- Registrar ou salvar dados (se necessário):
- Dependendo da aplicação, pode ser necessário registrar ou salvar os dados de frequência para análise posterior ou para manutenção de registros.
- Pós-processamento:
- Processamento adicional, como filtragem, média espectral ou análise harmônica, pode ser necessário dependendo da aplicação.
O que são equipamentos e ferramentas FFT?
Para medir a FFT, você pode usar vários equipamentos e ferramentas:
- Um osciloscópio digital com funcionalidade FFT.
- Um analisador de espectro dedicado, como Svantek
- Sistemas de aquisição de dados com ferramentas de software para análise FFT.
- Ferramentas de software como MATLAB, LabVIEW ou ferramentas baseadas em Python para análise de dados.

O que é o analisador FFT?
Um analisador FFT, ou analisador Fast Fourier Transform, é um dispositivo que fornece análise de frequência de sinais, comumente usado em áudio, estudos de vibração e várias outras aplicações. Ele usa o algoritmo FFT para transformar um sinal de seu domínio de tempo original para o domínio de frequência. Aqui está uma análise mais detalhada do que um analisador FFT faz:
- Conversão de domínio de tempo em frequência: A função principal de um analisador FFT é pegar um sinal no domínio do tempo (como uma gravação de áudio) e convertê-lo em sua representação no domínio da frequência. Isto permite aos usuários ver quais frequências estão presentes no sinal e em quais intensidades.
- Resolução: Os analisadores FFT fornecem uma visão do espectro onde os sinais são representados em termos de suas frequências constituintes. A resolução deste espectro pode variar de acordo com as configurações, especialmente o número de pontos FFT ou “linhas”.
- Filtragem e ponderação: A maioria dos analisadores FFT permite que os usuários apliquem diferentes filtros e ponderações ao sinal de entrada. Isto é especialmente relevante em aplicações como análise de áudio, onde os filtros de ponderação A, B, C ou Z podem ser aplicados para imitar a resposta do ouvido humano a diferentes frequências.
- Janelas: Para mitigar os efeitos do processamento de pedaços finitos de dados (que podem introduzir artefatos na análise de frequência), os analisadores FFT usam várias funções de janela, como Hanning, Rectangle, Flat Top ou Kaiser-Bessel.
- Aplicações: Os analisadores FFT são utilizados em uma variedade de campos, incluindo acústica (para analisar sinais de som ou ruído), análise de vibração (para determinar as frequências nas quais estruturas ou máquinas podem ressoar) e telecomunicações (para analisar o conteúdo de frequência de sinais).
- Análise em tempo real: Os analisadores FFT modernos podem fornecer análise de frequência em tempo real, permitindo aos usuários visualizar o conteúdo de frequência dos sinais à medida que eles mudam ao longo do tempo.
- Hardware e Software: Os analisadores FFT podem ser dispositivos de hardware independentes, geralmente com circuitos de entrada especializados para lidar com vários tipos de sinais. Eles também podem ser aplicativos de software executados em computadores padrão, usando entradas digitalizadas de placas de som ou outros dispositivos de entrada.
O que é um vazamento espectral?
Vazamento Espectral é um fenômeno que pode distorcer os resultados de uma análise FFT. Ao realizar uma FFT, existe uma suposição inerente de que o sinal no registro de tempo se repete indefinidamente. Contudo, esta suposição é violada se o número de ciclos do sinal nesse registro não for um número inteiro (não integral). Esta discrepância entre a repetição assumida e o sinal real pode levar ao vazamento espectral. O vazamento espectral pode manchar a energia de uma frequência específica em linhas ou compartimentos de frequência adjacentes, tornando o resultado menos preciso.
O que é Anti-Aliasing e Frequência Nyquist em relação à FFT?
Tanto o anti-aliasing quanto a frequência de Nyquist são conceitos cruciais para entender ao amostrar sinais e realizar análises FFT (Fast Fourier Transform):
- A Frequência Nyquist define a frequência máxima que pode ser amostrada com precisão e posteriormente reconstruída. Para capturar todos os detalhes de um sinal, é necessário amostrar pelo menos o dobro da frequência mais alta presente naquele sinal.
- Anti-aliasing é uma técnica para evitar a representação incorreta de frequências altas como frequências mais baixas em dados amostrados. Um filtro anti-aliasing garante que apenas frequências abaixo da frequência de Nyquist estejam presentes no sinal amostrado, salvaguardando assim a integridade do conteúdo de frequência do sinal no contexto da FFT e outras técnicas de processamento de sinal digital.
Por que a frequência de Nyquist é importante?
Ao amostrar um sinal contínuo para obter um sinal discreto para processamento digital (como FFT), o teorema de Nyquist (ou teorema de amostragem de Shannon-Nyquist) afirma que a frequência de amostragem deve ser pelo menos duas vezes a frequência mais alta presente no sinal para ser capaz de representar totalmente e posteriormente reconstruir o sinal contínuo original sem qualquer perda de informação. A frequência mais alta permitida no sinal, que é metade da taxa de amostragem, é a frequência de Nyquist. Matematicamente, se fS é a frequência de amostragem, a frequência de Nyquist fN é: fN=fS/2
Como funciona o anti-aliasing?
Para evitar aliasing, um filtro anti-aliasing é empregado. Este filtro é um filtro passa-baixa analógico aplicado ao sinal antes da amostragem. Sua finalidade é atenuar ou eliminar frequências no sinal que sejam superiores à frequência de Nyquist, garantindo assim que a versão amostrada do sinal não contenha informações de frequência enganosas. Ao fazer isso, garante que a versão discreta do sinal seja uma representação verdadeira do sinal contínuo até a frequência de Nyquist.
No contexto da FFT: Ao realizar uma FFT em dados amostrados, se os dados não tiverem sido amostrados corretamente (ou seja, em uma taxa alta o suficiente) ou se um filtro anti-aliasing apropriado não tiver sido aplicado, o espectro de frequência resultante pode contêm frequências com alias. Isto pode levar a interpretações incorretas ou enganosas do conteúdo de frequência do sinal.

Média dos espectros FFT
A média no contexto da FFT é usada para melhorar a relação sinal-ruído e fornecer uma representação mais precisa do espectro, especialmente ao analisar sinais não periódicos, como ruído ou música.
- A média clássica: conforme descrito no texto, um certo número de FFTs é capturado e então calculada a média. Cada resultado da FFT contribui igualmente para o espectro médio final. Este método é particularmente adequado para situações em que o sinal tem uma duração definida e o objetivo é obter uma representação média dessa duração.
- A média exponencial: Este é um tipo de média “ponderada”, onde os resultados recentes da FFT têm mais influência na média do que os mais antigos. Tal como o texto explica, a medição mais recente contribui de forma mais eficaz para a média, enquanto as medições mais antigas têm influência decrescente. Isto é particularmente útil ao monitorizar um espectro durante longos períodos, onde os dados recentes podem ser mais relevantes para o estado actual do que os dados mais antigos.
O que é áudio FFT?
FFT (Fast Fourier Transform) aplicado ao áudio refere-se ao processo de conversão de um sinal de áudio do domínio do tempo para o domínio da frequência. Esta transformação permite-nos ver os vários componentes de frequência (graves, médios, agudos, etc.) presentes num sinal de áudio a qualquer momento. Por exemplo, ao analisar uma peça musical, uma FFT irá quebrar o sinal para mostrar quanta energia existe em cada frequência. Isso poderia revelar o impacto de baixa frequência de um bumbo, os tons de frequência média de uma guitarra e o chiado de alta frequência de um prato, tudo ao mesmo tempo.
Analisador de áudio FFT
Um Analisador de Áudio FFT é uma ferramenta ou dispositivo que aplica o FFT a sinais de áudio, permitindo aos usuários visualizar o conteúdo de frequência do sinal. Essa visualização geralmente está na forma de um espectro, onde o eixo x representa a frequência (de baixa a alta) e o eixo y representa a amplitude (geralmente em uma escala logarítmica como dB). Os analisadores de áudio FFT são usados em uma variedade de aplicações:
- Acústica: Os engenheiros podem analisar a resposta de frequência de uma sala e projetar tratamentos acústicos de acordo.
- Teste de equipamentos de áudio: Os fabricantes podem testar a resposta de frequência de seus equipamentos, como alto-falantes e microfones.
- Análise de Ruído: Os profissionais podem identificar e medir ruídos indesejados em vários ambientes, desde fábricas até salas silenciosas.
- Análise da Fala: Estudar os padrões de frequência na fala pode ser útil em áreas como linguística e fonoaudiologia.
Audição Humana e Áudio FFT
A faixa de audição humana é geralmente considerada entre 20 Hz e 20.000 Hz (ou 20 kHz). Portanto, quando um Analisador de Áudio FFT é usado para analisar sinais de áudio destinados ao consumo humano (como música ou fala), o espectro de frequência normalmente se concentrará nesta faixa. É importante notar que embora possamos ouvir nesta faixa, a nossa sensibilidade às frequências não é uniforme. Os humanos são mais sensíveis a frequências entre 2 kHz e 4 kHz e menos sensíveis a frequências muito baixas e muito altas. Um analisador de áudio FFT representará todas as frequências com base em sua energia real no sinal, e não em como os humanos as percebem.
Importância de usar janelas FFT
O uso de janelas é crucial ao realizar medições baseadas em FFT. O Windows ajuda a mitigar certos problemas inerentes à natureza da FFT e às propriedades dos sinais em análise. Uma função de janelamento é uma função matemática aplicada ao sinal para mitigar os efeitos do vazamento espectral. Janelas diferentes têm propriedades diferentes e a escolha da janela afeta o resultado da análise FFT. O texto menciona três tipos específicos de janelas:
- Uniforme (Nenhum): Esta é essencialmente uma janela retangular, onde nenhuma função de janelamento é aplicada.
- Hanning (ou Hann): Esta é uma janela comumente usada que é um tipo de janela de cosseno. Ajuda a reduzir o vazamento espectral.
- Flat Top: Esta janela fornece medições de amplitude muito precisas, mas possui um lóbulo de frequência principal mais amplo.
Janelas diferentes são adequadas para cenários diferentes.
- Para amplos espectros de sinais, a janela Uniforme é ideal. Em muitos casos, a janela de Hann proporciona um bom equilíbrio.
- A janela Flat Top é precisa em amplitude, mas pior em resolução de frequência.
- Para sinais transitórios, são preferidas janelas especializadas como Força e Exponencial.

FFT em instrumentos Svantek
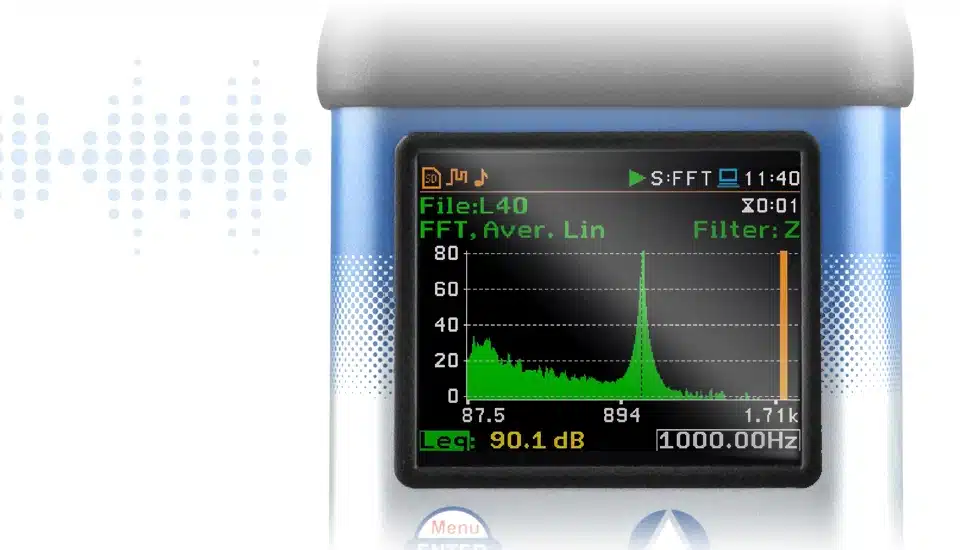
A FFT nos instrumentos Svantek permite que os usuários entendam os componentes de frequência dos sons ou vibrações que estão medindo. Isto é crucial para diversas aplicações, incluindo avaliações de ruído e vibração, solução de problemas e muito mais. Nos instrumentos Svantek, FFT (Fast Fourier Transform) é um algoritmo computacional que transforma um sinal de seu domínio original (domínio de tempo) em suas frequências constituintes. Ele fornece um meio de analisar os distintos componentes de frequência dos sinais, facilitando insights detalhados sobre as características das medições de som ou vibração. A funcionalidade FFT nos instrumentos Svantek opera em conjunto com seu medidor de nível e pode exibir resultados como espectros em uma visualização de espectro dedicada.
- Operação e exibição:
- O instrumento Svantek pode operar como um analisador FFT de maneira semelhante à funcionalidade do medidor de nível.
- A análise FFT é conduzida em paralelo com medições SLM (Sound Level Meter) ou VLM (Vibration Level Meter).
- Os resultados da análise FFT, denominados espectros, são mostrados na visualização Spectrum. Esta visualização permite aos usuários ler os valores do espectro com a ajuda de um cursor vertical.
- Configuração:
- Os usuários podem configurar vários parâmetros para a análise FFT. Isto inclui selecionar uma banda de frequência, definir um filtro de pré-ponderação, escolher uma janela de ponderação específica, determinar o número de linhas de análise e decidir sobre um tipo de média.
- Os espectros FFT podem ser calculados em média durante um período de integração designado e salvos de acordo com o parâmetro Repetition Cycles.
- A faixa de medição para FFT pode ser definida como Baixa ou Alta e, nos modos de vibração, os resultados podem ser exibidos em unidades absolutas ou logarítmicas.
- Registro:
- O instrumento suporta o registro de espectros FFT em um arquivo de registro. Isso pode ser feito em etapas definidas pelo Período de Integração ou pela Etapa Logger.
- Para registrar espectros FFT, a funcionalidade de registro deve estar habilitada no instrumento.
- Modos de exibição e apresentação:
- O instrumento oferece diversas configurações de exibição para os resultados FFT, permitindo aos usuários alternar entre diferentes visualizações, como espectros instantâneos, médios, máximos ou mínimos.
- Para aqueles que utilizam o instrumento em modos de vibração, podem selecionar o tipo de espectro de vibração a ser exibido, o que inclui opções como aceleração, velocidade ou deslocamento.
- Ferramentas:
- A posição do espectro nos modos de exibição ativa ou desativa a visualização do gráfico do espectro.
- Os usuários também podem definir a escala do gráfico do espectro, definindo as unidades de resultado (linear ou logarítmica) e ajustando o eixo vertical.
Aplicações da FFT da Svantek
Os recursos FFT da Svantek são voltados para análise acústica e de vibração, tornando seus instrumentos adequados para uma variedade de aplicações, desde estudos de ruído ambiental até monitoramento de máquinas industriais:
- Medição de nível sonoro: Os instrumentos Svantek realizam análises FFT em paralelo com medições de medidor de nível de som (SLM) ou medidor de nível de vibração (VLM), permitindo aos usuários obter informações detalhadas de frequência sobre sinais de som ou vibração juntamente com as medições de nível geral.
- Análise de vibração: A função FFT nos instrumentos Svantek pode ser usada em modos de vibração e os usuários podem alternar entre diferentes representações, como aceleração, velocidade ou deslocamento. Isto o torna adequado para analisar as características vibracionais de máquinas, estruturas ou outros sistemas.
- Vibração de edifícios: a FFT é usada de acordo com DIN 4150-3 para indicar a frequência dominante da velocidade máxima das partículas
- Análise Acústica: Com vários filtros de ponderação disponíveis (como ponderações A, B, C e Z), a funcionalidade FFT nos instrumentos Svantek pode ser usada para análise acústica detalhada.
- Visão do Espectro: Os instrumentos oferecem uma visão do espectro para os resultados da análise FFT. Isso permite aos usuários inspecionar visualmente os componentes de frequência do sinal analisado e compreender suas amplitudes relativas.
- Registro: Os espectros FFT podem ser registrados em um arquivo de registro, tornando-o adequado para aplicações onde o monitoramento de longo prazo e o registro de dados são necessários. Isto pode ser especialmente útil em estudos de ruído ambiental, monitoramento industrial ou qualquer cenário onde as tendências ao longo do tempo sejam de interesse.
- Análise de banda de frequência: Os usuários podem selecionar bandas de frequência específicas para desempenho de análise FFT, de 20 kHz a 78 Hz. Isso fornece flexibilidade no zoom em faixas de frequência específicas de interesse.
- Configurabilidade para diferentes necessidades de análise: Com opções para configurar parâmetros como banda de frequência, filtro de pré-ponderação, janela de ponderação, número de linhas e tipo de média, a funcionalidade Svantek FFT pode ser adaptada para diversas aplicações especializadas.
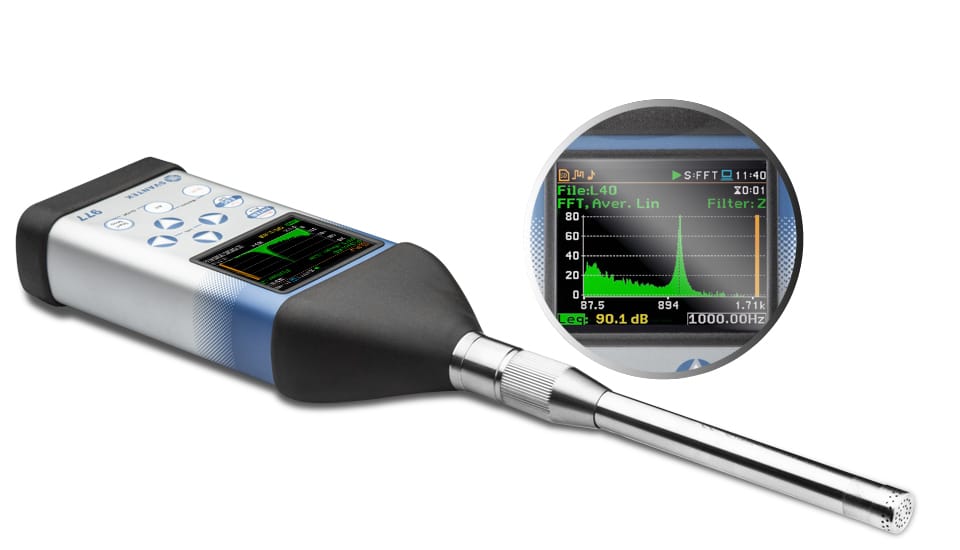
Método FFT em vibração de edifícios
O método FFT na vibração de edifícios é descrito na norma alemã DIN 4150-3. O método requer a realização de análise FFT para o Pico de Velocidade de Partículas (PPV), de forma que o meio de uma janela FFT seja colocado exatamente no PPV. O resultado desta análise é o valor do PPV e sua correspondente Frequência Dominante (DF) para cada eixo (X,Y,Z). Cada par de PPV e seu DF são usados como coordenadas de ponto que são comparadas com a curva limite.
Resumo
Transformada Rápida de Fourier FFT: Principais vantagens:
- FFT Fast Fourier Transform é um algoritmo para cálculo eficiente da DFT e seu inverso.
- DFT é usado para transformar sinais em sua representação no domínio da frequência.
- A FFT acelera a computação DFT, permitindo aplicações em tempo real e grandes conjuntos de dados.
- A FFT foi co-descoberta por Cooley e Tukey em 1965, revolucionando o processamento digital de sinais.
- As aplicações FFT abrangem mecânica, acústica, engenharia biomédica, processamento de sinais, instrumentação, comunicações e muito mais.
- Os benefícios do uso de FFT incluem análise de sinal, redução de ruído, compressão, design de filtro e muito mais.
- A FFT converte sinais do domínio do tempo para o domínio da frequência e vice-versa.
- A frequência Nyquist é essencial para uma amostragem precisa, enquanto o anti-aliasing evita erros nos dados amostrados.
- A FFT pode ser realizada em tempo real ou pós-processamento, dependendo da aplicação.
- A média dos espectros FFT aumenta a relação sinal-ruído para sinais não periódicos.
- Diferentes janelas (uniforme, Hanning, Flat Top) ajudam a mitigar o vazamento espectral na análise FFT.
- A Svantek Instruments utiliza FFT para análise de som e vibração em diversas aplicações.