Transformada rápida de Fourier FFT
La transformada rápida de Fourier FFT permite la descomposición de señales en sus sinusoides constituyentes, lo que permite el análisis en el dominio de la frecuencia.
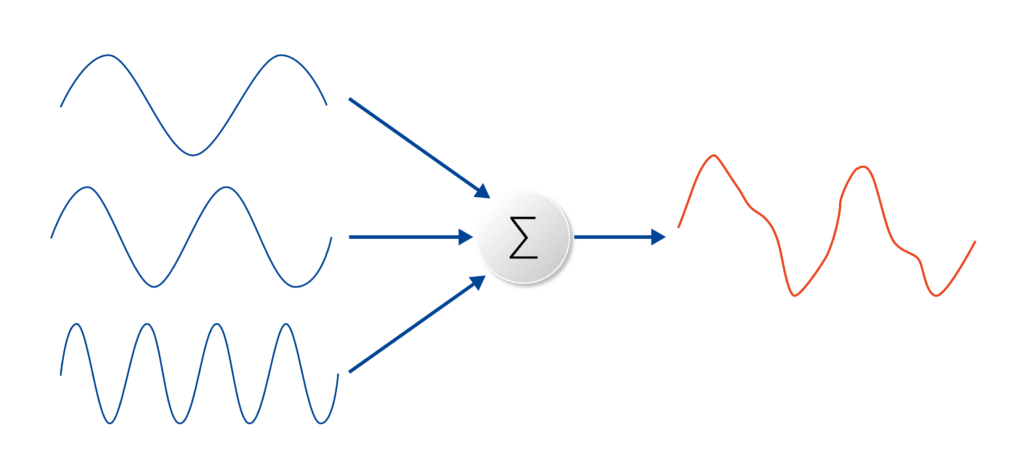
La transformada rápida de Fourier FFT permite la descomposición de señales en sus sinusoides constituyentes, lo que permite el análisis en el dominio de la frecuencia.
La transformada rápida de Fourier FFT es un algoritmo utilizado para calcular la transformada discreta de Fourier (DFT) y su inversa de manera más eficiente. La DFT es una transformada utilizada en el procesamiento de señales y de imágenes, entre muchas otras áreas, para transformar una señal discreta en su representación en el dominio de la frecuencia. La FFT acelera el proceso de cálculo de la DFT, lo que permite su uso en aplicaciones en tiempo real y para grandes conjuntos de datos.
La FFT fue descubierta conjuntamente por James W. Cooley y John W. Tukey en 1965. Si bien el algoritmo fue ciertamente un gran avance, cabe señalar que muchas de sus ideas fundamentales existían desde hacía algún tiempo, pero el trabajo de Cooley y Tukey trajo a la prominencia en la era digital, especialmente con el auge de la informática digital. Su versión del algoritmo redujo en gran medida la complejidad computacional del procesamiento de grandes conjuntos de datos, lo que hizo que el procesamiento de señales digitales fuera más factible y eficiente.
La FFT es un algoritmo optimizado diseñado para calcular rápidamente la Transformada Discreta de Fourier (DFT) y su inversa. La ventaja de la FFT radica en su eficiencia. Si bien un cálculo directo de la DFT requiere operaciones O(N^2) (tiempo cuadrático), el algoritmo FFT permite el mismo cálculo en operaciones O(N log N), lo que supone una aceleración significativa para grandes conjuntos de datos.
El algoritmo FFT (Transformada Rápida de Fourier) se utiliza en una amplia gama de aplicaciones porque puede convertir una señal de su dominio de tiempo a su dominio de frecuencia, y viceversa. Comprender los componentes de frecuencia de una señal puede proporcionar información valiosa sobre la naturaleza, el comportamiento y las propiedades de esa señal.
¿Qué es la ecuación FFT?
La FFT es un algoritmo que calcula eficientemente la DFT, por lo que la ecuación es la misma que la ecuación DFT. Sin embargo, vale la pena señalar que existen muchos algoritmos FFT diferentes (por ejemplo, radix-2, split-radix, etc.) y cada uno tiene sus propios pasos y complejidades específicos.
¿Qué es el DFT?
DFT Discrete Fourier Transform es una poderosa herramienta matemática que se utiliza para transformar señales periódicas discretas de su representación en el dominio del tiempo a una representación en el dominio de la frecuencia. Esto permite el análisis y la manipulación en el dominio de la frecuencia antes de volver a transformarse potencialmente al dominio del tiempo con la DFT inversa. La DFT, que la FFT calcula de manera eficiente, se define para una secuencia x[n] de longitud N como:
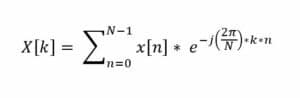
Dónde:
e es la base del logaritmo natural (aproximadamente igual a 2,71828).
Hay muchas aplicaciones FFT:
Existen muchos beneficios de utilizar FFT en diversas aplicaciones:
La Transformada de Fourier es un concepto matemático más amplio que se utiliza para transformar señales entre los dominios de tiempo (o espacial) y frecuencia. La Transformada Rápida de Fourier es un algoritmo específico y optimizado para calcular la DFT, que es la versión muestreada de FT, de una manera más rápida.
La transformada de Fourier descompone una forma de onda en una suma de sinusoides de diferentes frecuencias. Esto significa que la transformada de Fourier representa la misma información que la forma de onda original, sólo que en el dominio de la frecuencia (a diferencia del dominio del tiempo). La metodología del análisis de la transformada de Fourier es esencial para la resolución eficaz de problemas en muchos contextos científicos y de ingeniería. Visualmente, la transformada de Fourier está representada por un diagrama que indica la amplitud y frecuencia de cada sinusoide. La siguiente ecuación representa la transformada de Fourier de tiempo continuo. La ecuación captura cómo cualquier señal de tiempo continuo se puede representar como una suma (integral) de sinusoides de todas las frecuencias posibles:
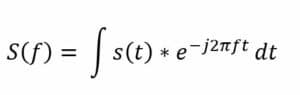
Dónde:
La Transformada Rápida de Fourier (FFT) se puede aplicar tanto en contextos de posprocesamiento como en tiempo real. La distinción entre ambos depende principalmente de la aplicación y de los requisitos específicos de la tarea en cuestión.
FFT en tiempo real:
FFT de posprocesamiento:
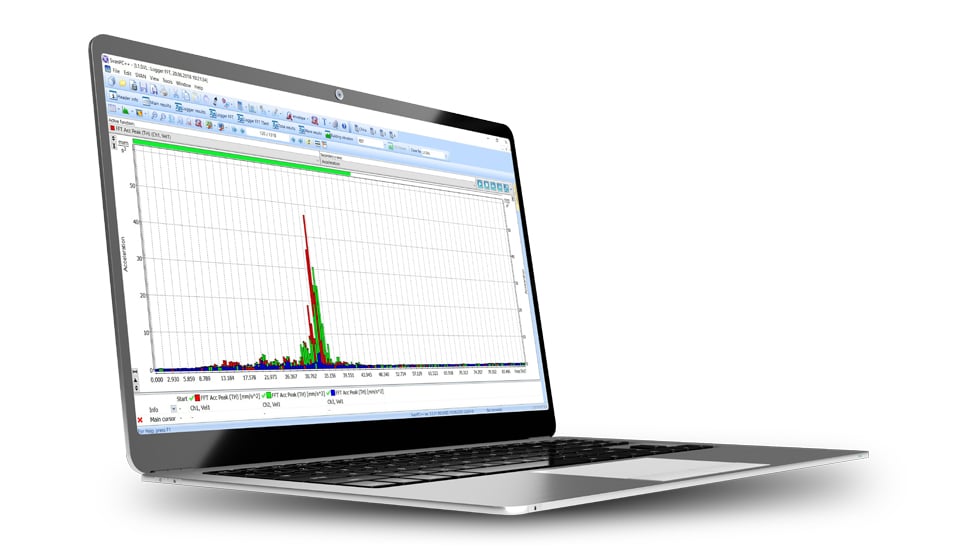
Medir la FFT (Transformada Rápida de Fourier) implica capturar una señal en el dominio del tiempo y luego transformarla en el dominio de la frecuencia para analizar sus componentes de frecuencia. Aquí hay una guía básica paso a paso sobre cómo medir FFT:
Para medir FFT, puede utilizar varios equipos y herramientas:
Un analizador FFT, o analizador de transformada rápida de Fourier, es un dispositivo que proporciona análisis de frecuencia de señales, comúnmente utilizado en audio, estudios de vibración y varias otras aplicaciones. Utiliza el algoritmo FFT para transformar una señal de su dominio de tiempo original al dominio de frecuencia. Aquí hay un desglose más detallado de lo que hace un analizador FFT:
La fuga espectral es un fenómeno que puede sesgar los resultados de un análisis FFT. Al realizar una FFT, existe la suposición inherente de que la señal en el registro de tiempo se repite indefinidamente. Sin embargo, esta suposición se viola si el número de ciclos de la señal en ese registro no es un número entero (no integral). Esta discrepancia entre la repetición supuesta y la señal real puede provocar una fuga espectral. La fuga espectral puede difundir la energía de una frecuencia específica a través de líneas o contenedores de frecuencia adyacentes, lo que hace que el resultado sea menos preciso.
Tanto el antialiasing como la frecuencia de Nyquist son conceptos cruciales que se deben comprender al muestrear señales y realizar análisis FFT (Transformada Rápida de Fourier):
Al muestrear una señal continua para obtener una señal discreta para procesamiento digital (como FFT), el teorema de Nyquist (o teorema de muestreo de Shannon-Nyquist) establece que la frecuencia de muestreo debe ser al menos el doble de la frecuencia más alta presente en la señal para poder representar completamente y luego reconstruir la señal continua original sin pérdida de información. La frecuencia más alta permitida en la señal, que es la mitad de la frecuencia de muestreo, es la frecuencia de Nyquist. Matemáticamente, si fS es la frecuencia de muestreo, la frecuencia de Nyquist fN es: fN=fS/2
Para evitar el aliasing, se emplea un filtro antialiasing. Este filtro es un filtro analógico de paso bajo que se aplica a la señal antes del muestreo. Su propósito es atenuar o eliminar frecuencias en la señal que son más altas que la frecuencia de Nyquist, asegurando así que la versión muestreada de la señal no contenga información de frecuencia engañosa. Al hacerlo, garantiza que la versión discreta de la señal sea una representación real de la señal continua hasta la frecuencia de Nyquist.
En el contexto de FFT: al realizar una FFT en datos muestreados, si los datos no se han muestreado correctamente (es decir, a una velocidad suficientemente alta) o si no se ha aplicado un filtro anti-aliasing adecuado, el espectro de frecuencia resultante puede contienen frecuencias con alias. Esto puede dar lugar a interpretaciones incorrectas o engañosas del contenido de frecuencia de la señal.
El promedio en el contexto de FFT se utiliza para mejorar la relación señal-ruido y proporcionar una representación más precisa del espectro, especialmente cuando se analizan señales no periódicas como el ruido o la música.
FFT (Transformada Rápida de Fourier) aplicada al audio se refiere al proceso de convertir una señal de audio del dominio del tiempo al dominio de la frecuencia. Esta transformación nos permite ver los distintos componentes de frecuencia (graves, medios, agudos, etc.) presentes en una señal de audio en un momento dado. Por ejemplo, al analizar una pieza musical, una FFT descompondrá la señal para mostrar cuánta energía existe en cada frecuencia. Esto podría revelar el golpe de baja frecuencia de un bombo, los tonos de frecuencia media de una guitarra y el chisporroteo de alta frecuencia de un platillo, todo al mismo tiempo.
Un analizador de audio FFT es una herramienta o dispositivo que aplica FFT a señales de audio, permitiendo a los usuarios visualizar el contenido de frecuencia de la señal. Esta visualización suele tener la forma de un espectro, donde el eje x representa la frecuencia (de baja a alta) y el eje y representa la amplitud (a menudo en una escala logarítmica como dB). Los analizadores de audio FFT se utilizan en una variedad de aplicaciones:
Generalmente se considera que el rango de audición humana es de 20 Hz a 20.000 Hz (o 20 kHz). Por lo tanto, cuando se utiliza un analizador de audio FFT para analizar señales de audio destinadas al consumo humano (como música o voz), el espectro de frecuencia normalmente se centrará en este rango. Vale la pena señalar que, si bien podemos oír en este rango, nuestra sensibilidad a las frecuencias no es uniforme. Los humanos son más sensibles a frecuencias entre 2 kHz y 4 kHz y menos sensibles a frecuencias muy bajas y muy altas. Un analizador de audio FFT representará todas las frecuencias en función de su energía real en la señal, no de cómo las perciben los humanos.
El uso de ventanas es crucial al realizar mediciones basadas en FFT. Windows ayuda a mitigar ciertos problemas inherentes a la naturaleza de FFT y las propiedades de las señales bajo análisis. Una función de ventana es una función matemática que se aplica a la señal para mitigar los efectos de la fuga espectral. Diferentes ventanas tienen diferentes propiedades y la elección de la ventana afecta el resultado del análisis FFT. El texto menciona tres tipos específicos de ventanas:
Diferentes ventanas son adecuadas para diferentes escenarios.
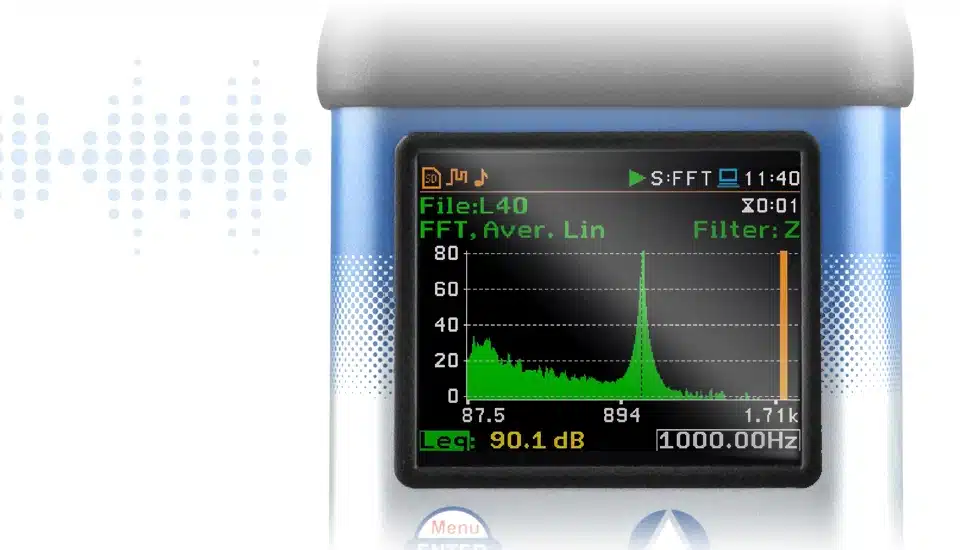
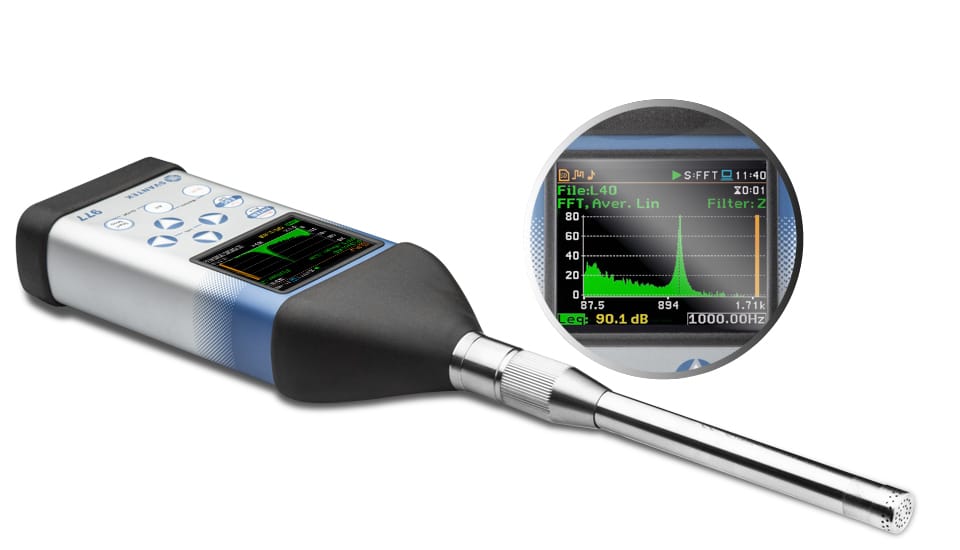
FFT en los instrumentos Svantek permite a los usuarios comprender los componentes de frecuencia de los sonidos o vibraciones que están midiendo. Esto es crucial para diversas aplicaciones, incluidas evaluaciones de ruido y vibraciones, resolución de problemas y más. En los instrumentos Svantek, FFT (Fast Fourier Transform) es un algoritmo computacional que transforma una señal de su dominio original (dominio del tiempo) en sus frecuencias constituyentes. Proporciona un medio para analizar los distintos componentes de frecuencia de las señales, facilitando información detallada sobre las características de las mediciones de sonido o vibración. La funcionalidad FFT en los instrumentos Svantek funciona junto con su medidor de nivel y puede mostrar resultados como espectros en una vista de espectro dedicada.
Las capacidades FFT de Svantek están orientadas al análisis acústico y de vibraciones, lo que hace que sus instrumentos sean adecuados para una variedad de aplicaciones, desde estudios de ruido ambiental hasta monitoreo de máquinas industriales:
El método FFT para la vibración de edificios se describe en la norma alemana DIN 4150-3. El método requiere realizar un análisis FFT para la velocidad máxima de partículas (PPV), de manera que el centro de una ventana FFT se coloque exactamente en el PPV. El resultado de dicho análisis es el valor de PPV y su correspondiente Frecuencia Dominante (DF) para cada eje (X,Y,Z). Cada par de PPV y su DF se utilizan como coordenadas de puntos que se comparan con la curva límite.
Resumen
Transformada rápida de Fourier FFT: conclusiones clave:
Un consultor autorizado de SVANTEK le ayudará con los detalles, como los accesorios necesarios para su tarea de monitoreo de ruido y vibraciones.
