Trasformata veloce di Fourier FFT
La trasformata veloce di Fourier FFT consente la scomposizione dei segnali nelle sinusoidi costituenti, consentendo l’analisi nel dominio della frequenza.
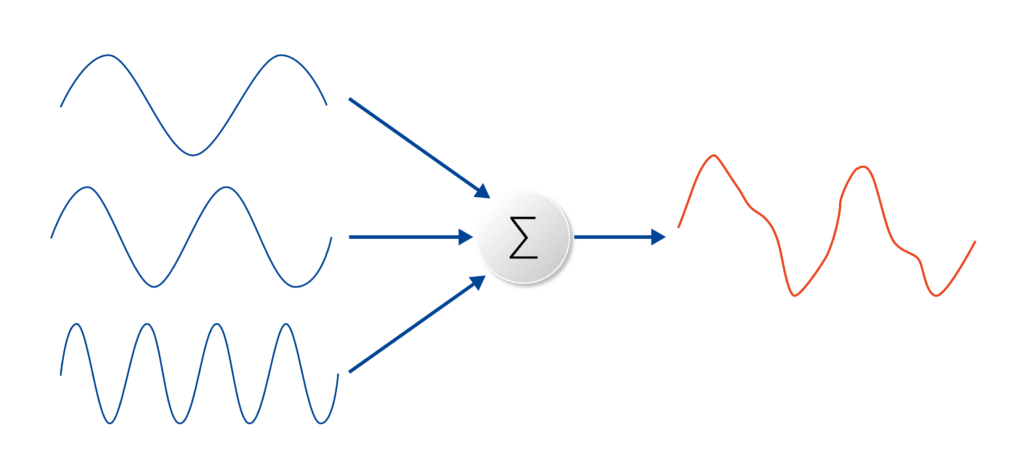
La trasformata veloce di Fourier FFT consente la scomposizione dei segnali nelle sinusoidi costituenti, consentendo l’analisi nel dominio della frequenza.
La trasformata veloce di Fourier FFT è un algoritmo utilizzato per calcolare la trasformata discreta di Fourier (DFT) e la sua inversa in modo più efficiente. La DFT è una trasformazione utilizzata nell’elaborazione del segnale e nell’elaborazione delle immagini, tra molte altre aree, per trasformare un segnale discreto nella sua rappresentazione nel dominio della frequenza. La FFT accelera il processo di calcolo della DFT, consentendone l’utilizzo in applicazioni in tempo reale e per set di dati di grandi dimensioni.
La FFT è stata scoperta congiuntamente da James W. Cooley e John W. Tukey nel 1965. Sebbene l’algoritmo abbia rappresentato certamente una svolta, va notato che molte delle sue idee fondamentali erano in circolazione da qualche tempo, ma il lavoro di Cooley e Tukey ha portato alla ribalta nell’era digitale, soprattutto con l’avvento dell’informatica digitale. La loro versione dell’algoritmo ha ridotto notevolmente la complessità computazionale dell’elaborazione di grandi set di dati, rendendo l’elaborazione del segnale digitale più fattibile ed efficiente.
La FFT è un algoritmo ottimizzato progettato per calcolare rapidamente la trasformata discreta di Fourier (DFT) e la sua inversa. Il vantaggio della FFT risiede nella sua efficienza. Mentre un calcolo diretto della DFT richiede operazioni O(N^2) (tempo quadratico), l’algoritmo FFT consente lo stesso calcolo in operazioni O(N log N), il che rappresenta un notevole aumento di velocità per set di dati di grandi dimensioni.
L’algoritmo FFT (Fast Fourier Transform) viene utilizzato in una vasta gamma di applicazioni perché può convertire un segnale dal suo dominio del tempo al dominio della frequenza e viceversa. Comprendere le componenti di frequenza di un segnale può fornire preziose informazioni sulla natura, il comportamento e le proprietà di quel segnale.
Qual è l'equazione FFT?
La FFT è un algoritmo che calcola in modo efficiente la DFT, quindi l’equazione è la stessa dell’equazione DFT. Tuttavia, vale la pena notare che esistono molti algoritmi FFT diversi (ad esempio, radix-2, split-radix, ecc.) e ognuno ha i propri passaggi e complessità specifici.
Cos'è il DFT?
La trasformata discreta di Fourier DFT è un potente strumento matematico utilizzato per trasformare segnali periodici discreti dalla loro rappresentazione nel dominio del tempo a una rappresentazione nel dominio della frequenza. Ciò consente l’analisi e la manipolazione nel dominio della frequenza prima di tornare potenzialmente nel dominio del tempo con la DFT inversa. La DFT, che la FFT calcola in modo efficiente, è definita per una sequenza x[n] di lunghezza N come:
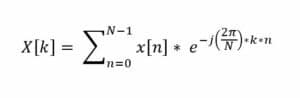
Dove:
e è la base del logaritmo naturale (pari a circa 2,71828).
Esistono molte applicazioni FFT:
Ci sono molti vantaggi nell’utilizzare la FFT in varie applicazioni:
La trasformata di Fourier è un concetto matematico più ampio utilizzato per trasformare i segnali tra i domini temporali (o spaziali) e di frequenza, la trasformata veloce di Fourier è un algoritmo specifico e ottimizzato per calcolare la DFT, che è la versione campionata di FT, in modo più veloce.
La trasformata di Fourier decompone una forma d’onda in una somma di sinusoidi di frequenze diverse. Ciò significa che la trasformata di Fourier rappresenta le stesse informazioni della forma d’onda originale, solo nel dominio della frequenza (in contrapposizione al dominio del tempo). La metodologia dell’analisi della trasformata di Fourier è essenziale per un’efficace risoluzione dei problemi in molti contesti ingegneristici e scientifici. Visivamente, la trasformata di Fourier è rappresentata da un diagramma che indica l’ampiezza e la frequenza di ciascuna sinusoide. L’equazione seguente rappresenta la trasformata di Fourier a tempo continuo. L’equazione cattura come qualsiasi segnale a tempo continuo possa essere rappresentato come una somma (integrale) di sinusoidi di tutte le possibili frequenze:
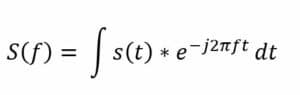
Dove:
La Trasformata Veloce di Fourier (FFT) può essere applicata sia in contesti in tempo reale che in post-elaborazione. La distinzione tra i due dipende principalmente dall’applicazione e dai requisiti specifici del compito da svolgere.
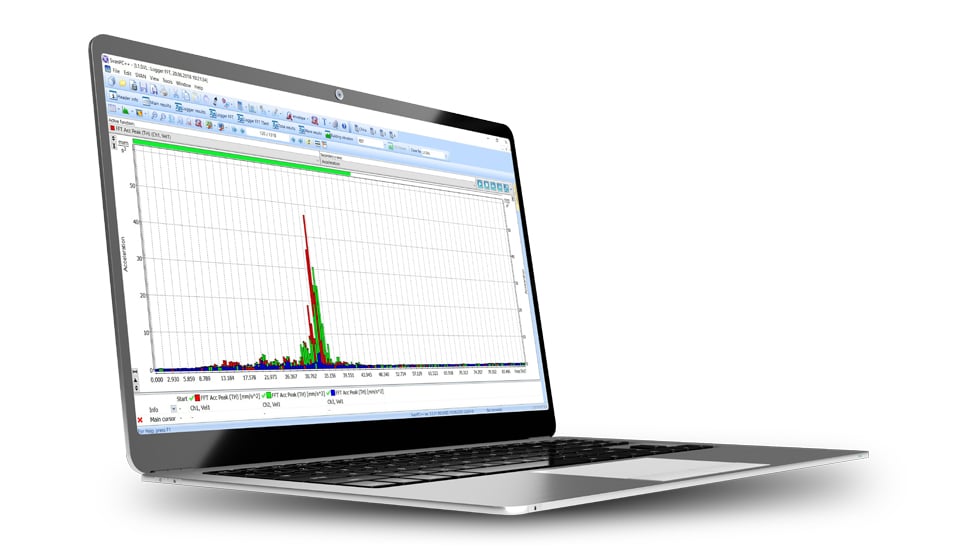
Misurare la FFT (Fast Fourier Transform) implica catturare un segnale nel dominio del tempo e quindi trasformarlo nel dominio della frequenza per analizzarne le componenti di frequenza. Ecco una guida passo passo di base su come misurare la FFT:
Per misurare la FFT, è possibile utilizzare varie apparecchiature e strumenti:
Un analizzatore FFT, o analizzatore di trasformata veloce di Fourier, è un dispositivo che fornisce l’analisi della frequenza dei segnali, comunemente utilizzato negli studi sull’audio, sulle vibrazioni e in varie altre applicazioni. Utilizza l’algoritmo FFT per trasformare un segnale dal suo dominio temporale originale nel dominio della frequenza. Ecco una ripartizione più dettagliata di ciò che fa un analizzatore FFT:
La perdita spettrale è un fenomeno che può distorcere i risultati di un’analisi FFT. Quando si esegue una FFT, si presuppone intrinsecamente che il segnale nella registrazione del tempo si ripeta indefinitamente. Tuttavia, questo presupposto viene violato se il numero di cicli del segnale in quella registrazione non è un numero intero (non intero). Questa discrepanza tra la ripetizione presunta e il segnale reale può portare a una perdita spettrale. La dispersione spettrale può diffondere l’energia da una frequenza specifica attraverso linee o contenitori di frequenza adiacenti, rendendo il risultato meno accurato.
Sia l’anti-aliasing che la frequenza di Nyquist sono concetti cruciali da comprendere durante il campionamento dei segnali e l’esecuzione di analisi FFT (Fast Fourier Transform):
Quando si campiona un segnale continuo per ottenere un segnale discreto per l’elaborazione digitale (come FFT), il teorema di Nyquist (o teorema di campionamento di Shannon-Nyquist) afferma che la frequenza di campionamento deve essere almeno il doppio della frequenza più alta presente nel segnale per poter rappresentare completamente e successivamente ricostruire il segnale continuo originale senza alcuna perdita di informazioni. La frequenza più alta consentita nel segnale, che è la metà della frequenza di campionamento, è la frequenza Nyquist. Matematicamente, se fS è la frequenza di campionamento, la frequenza di Nyquist fN è: fN=fS/2
Per prevenire l’aliasing, viene utilizzato un filtro anti-aliasing. Questo filtro è un filtro passa-basso analogico applicato al segnale prima del campionamento. Il suo scopo è attenuare o eliminare le frequenze nel segnale superiori alla frequenza di Nyquist, garantendo così che la versione campionata del segnale non contenga informazioni di frequenza fuorvianti. In questo modo si garantisce che la versione discreta del segnale sia una rappresentazione fedele del segnale continuo fino alla frequenza di Nyquist.
Nel contesto della FFT: quando si esegue una FFT sui dati campionati, se i dati non sono stati campionati correttamente (cioè a una velocità sufficientemente elevata) o se non è stato applicato un filtro anti-aliasing appropriato, lo spettro di frequenza risultante può contengono frequenze con alias. Ciò può portare a interpretazioni errate o fuorvianti del contenuto in frequenza del segnale.
La media nel contesto della FFT viene utilizzata per migliorare il rapporto segnale-rumore e fornire una rappresentazione più accurata dello spettro, soprattutto quando si analizzano segnali non periodici come rumore o musica.
La FFT (Fast Fourier Transform) applicata all’audio si riferisce al processo di conversione di un segnale audio dal dominio del tempo al dominio della frequenza. Questa trasformazione ci permette di vedere le varie componenti di frequenza (bassi, medi, alti, ecc.) presenti in un segnale audio in un dato momento. Ad esempio, quando si analizza un brano musicale, una FFT scompone il segnale per mostrare quanta energia esiste a ciascuna frequenza. Ciò potrebbe rivelare il tonfo a bassa frequenza di una grancassa, i toni a media frequenza di una chitarra e lo sfrigolio ad alta frequenza di un piatto, tutto allo stesso tempo.
Un analizzatore audio FFT è uno strumento o dispositivo che applica la FFT ai segnali audio, consentendo agli utenti di visualizzare il contenuto in frequenza del segnale. Questa visualizzazione è spesso sotto forma di uno spettro, dove l’asse x rappresenta la frequenza (dal basso all’alto) e l’asse y rappresenta l’ampiezza (spesso in scala logaritmica come dB). Gli analizzatori audio FFT sono utilizzati in una vasta gamma di applicazioni:
La gamma uditiva umana è generalmente considerata compresa tra 20 Hz e 20.000 Hz (o 20 kHz). Pertanto, quando un analizzatore audio FFT viene utilizzato per analizzare segnali audio destinati al consumo umano (come musica o parlato), lo spettro di frequenza si concentrerà generalmente su questa gamma. Vale la pena notare che mentre possiamo sentire in questa gamma, la nostra sensibilità alle frequenze non è uniforme. Gli esseri umani sono più sensibili alle frequenze comprese tra 2 kHz e 4 kHz e meno sensibili alle frequenze molto basse e molto alte. Un analizzatore audio FFT rappresenterà tutte le frequenze in base alla loro effettiva energia nel segnale, non a come gli esseri umani le percepiscono.
L’uso delle finestre è fondamentale quando si eseguono misurazioni basate su FFT. Windows aiuta a mitigare alcuni problemi inerenti alla natura della FFT e alle proprietà dei segnali in analisi. Una funzione di finestra è una funzione matematica applicata al segnale per mitigare gli effetti della perdita spettrale. Finestre diverse hanno proprietà diverse e la scelta della finestra influisce sul risultato dell’analisi FFT. Il testo menziona tre tipi specifici di finestre:
Finestre diverse sono adatte a scenari diversi.
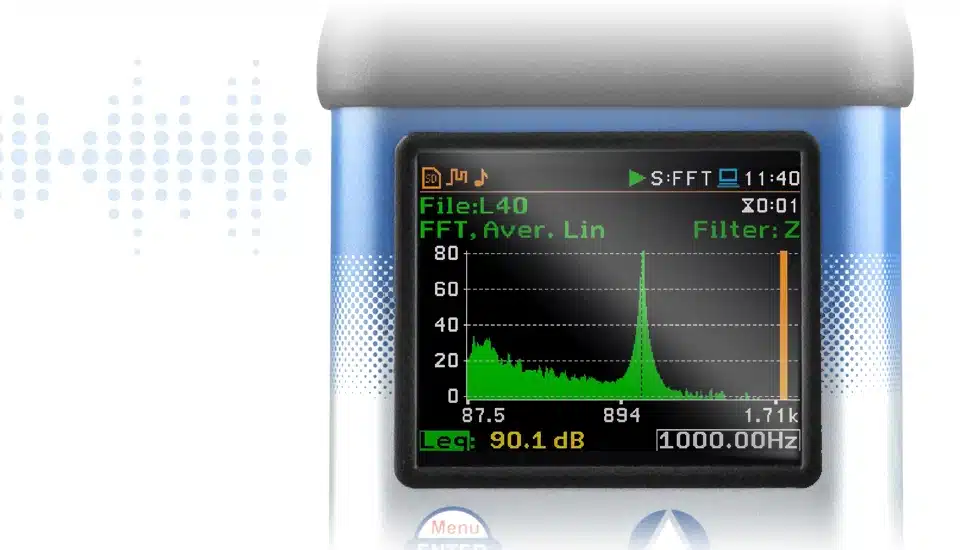
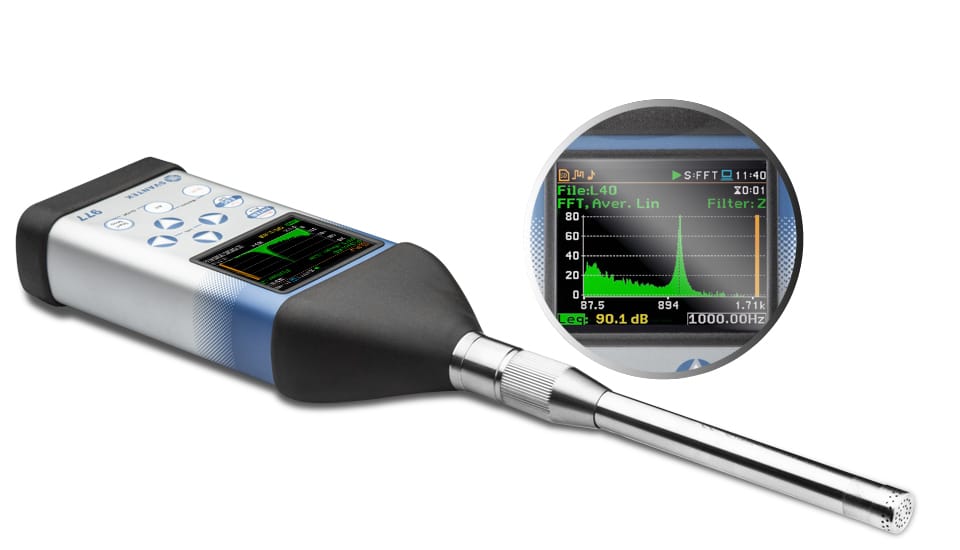
La FFT negli strumenti Svantek consente agli utenti di comprendere le componenti di frequenza dei suoni o delle vibrazioni che stanno misurando. Ciò è fondamentale per varie applicazioni, tra cui la valutazione del rumore e delle vibrazioni, la risoluzione dei problemi e altro ancora. Negli strumenti Svantek, la FFT (Fast Fourier Transform) è un algoritmo computazionale che trasforma un segnale dal suo dominio originale (dominio temporale) nelle sue frequenze costituenti. Fornisce un mezzo per analizzare le distinte componenti di frequenza dei segnali, facilitando approfondimenti dettagliati sulle caratteristiche delle misurazioni del suono o delle vibrazioni. La funzionalità FFT negli strumenti Svantek funziona insieme al misuratore di livello e può visualizzare i risultati come spettri in una vista Spettro dedicata.
Le capacità FFT di Svantek sono orientate all’analisi sia acustica che delle vibrazioni, rendendo i suoi strumenti adatti a una varietà di applicazioni, dagli studi sul rumore ambientale al monitoraggio delle macchine industriali:
Il metodo FFT per le vibrazioni degli edifici è descritto nella norma tedesca DIN 4150-3. Il metodo richiede di eseguire l’analisi FFT per la velocità di picco delle particelle (PPV), in modo che il centro di una finestra FFT sia posizionato esattamente sul PPV. Il risultato di tale analisi è il valore PPV e la corrispondente frequenza dominante (DF) per ciascun asse (X,Y,Z). Ciascuna coppia di PPV e il relativo DF vengono utilizzati come coordinate del punto confrontate con la curva limite.
Riepilogo
Trasformata veloce di Fourier FFT: punti chiave:
Un consulente SVANTEK autorizzato ti aiuterà con i dettagli, come gli accessori necessari per il tuo compito di monitoraggio del rumore e delle vibrazioni.
