FFT Schnelle Fourier-Transformation
Die FFT-Fast-Fourier-Transformation ermöglicht die Zerlegung von Signalen in ihre Sinuskurven und ermöglicht so eine Analyse im Frequenzbereich.
Die FFT-Fast-Fourier-Transformation ermöglicht die Zerlegung von Signalen in ihre Sinuskurven und ermöglicht so eine Analyse im Frequenzbereich.
Die FFT-Fast-Fourier-Transformation ist ein Algorithmus zur effizienteren Berechnung der diskreten Fourier-Transformation (DFT) und ihrer Umkehrung. Die DFT ist eine Transformation, die neben vielen anderen Bereichen in der Signalverarbeitung und Bildverarbeitung verwendet wird, um ein diskretes Signal in seine Frequenzbereichsdarstellung umzuwandeln. Die FFT beschleunigt den Berechnungsprozess der DFT und ermöglicht so den Einsatz in Echtzeitanwendungen und für große Datensätze.
Die FFT wurde 1965 von James W. Cooley und John W. Tukey gemeinsam entdeckt. Obwohl der Algorithmus sicherlich ein Durchbruch war, sollte beachtet werden, dass viele seiner grundlegenden Ideen schon seit einiger Zeit existierten, aber die Arbeit von Cooley und Tukey brachte Es erlangte im digitalen Zeitalter, insbesondere mit dem Aufkommen der digitalen Datenverarbeitung, zunehmende Bedeutung. Ihre Version des Algorithmus reduzierte die Rechenkomplexität bei der Verarbeitung großer Datensätze erheblich und machte die digitale Signalverarbeitung praktikabler und effizienter.
Die FFT ist ein optimierter Algorithmus zur schnellen Berechnung der Diskreten Fourier-Transformation (DFT) und ihrer Umkehrung. Der Vorteil der FFT liegt in ihrer Effizienz. Während eine direkte Berechnung der DFT O(N^2) Operationen (quadratische Zeit) erfordert, ermöglicht der FFT-Algorithmus die gleiche Berechnung in O(N log N) Operationen, was eine erhebliche Beschleunigung für große Datensätze darstellt.
Der FFT-Algorithmus (Fast Fourier Transform) wird in einer Vielzahl von Anwendungen eingesetzt, da er ein Signal von seinem Zeitbereich in seinen Frequenzbereich und umgekehrt umwandeln kann. Das Verständnis der Frequenzkomponenten eines Signals kann wertvolle Einblicke in die Natur, das Verhalten und die Eigenschaften dieses Signals liefern.
Was ist die FFT-Gleichung?
Die FFT ist ein Algorithmus, der die DFT effizient berechnet, daher ist die Gleichung dieselbe wie die DFT-Gleichung. Es ist jedoch erwähnenswert, dass es viele verschiedene FFT-Algorithmen gibt (z. B. Radix-2, Split-Radix usw.) und jeder seine eigenen spezifischen Schritte und Feinheiten hat.
Was ist die DFT?
Die diskrete Fourier-Transformation DFT ist ein leistungsstarkes mathematisches Werkzeug, mit dem diskrete, periodische Signale von ihrer Zeitbereichsdarstellung in eine Frequenzbereichsdarstellung umgewandelt werden. Dies ermöglicht eine Analyse und Manipulation im Frequenzbereich, bevor möglicherweise mit der inversen DFT zurück in den Zeitbereich transformiert wird. Die DFT, die die FFT effizient berechnet, ist für eine Folge x[n] der Länge N wie folgt definiert:
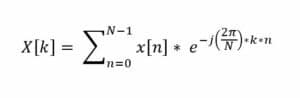
Wo:
e ist die Basis des natürlichen Logarithmus (ungefähr gleich 2,71828).
Es gibt viele FFT-Anwendungen:
Der Einsatz von FFT in verschiedenen Anwendungen bietet viele Vorteile:
Die Fourier-Transformation ist ein umfassenderes mathematisches Konzept zur Transformation von Signalen zwischen Zeit- (oder räumlichen) und Frequenzbereichen. Die schnelle Fourier-Transformation ist ein spezifischer, optimierter Algorithmus zur schnelleren Berechnung der DFT, der abgetasteten Version von FT.
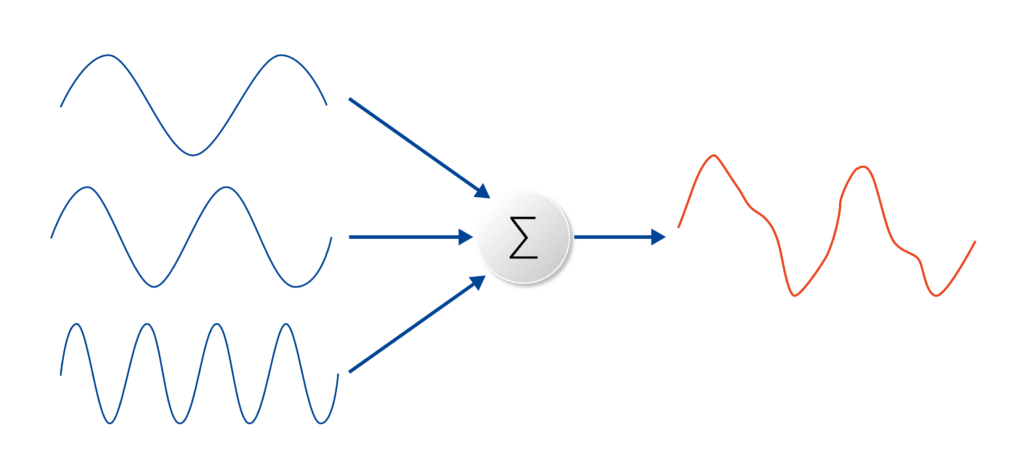
Die Fourier-Transformation zerlegt eine Wellenform in eine Summe von Sinuskurven unterschiedlicher Frequenz. Das bedeutet, dass die Fourier-Transformation dieselben Informationen wie die ursprüngliche Wellenform darstellt, nur im Frequenzbereich (im Gegensatz zum Zeitbereich). Die Methodik der Fourier-Transformationsanalyse ist für eine effektive Problemlösung in vielen technischen und wissenschaftlichen Kontexten von wesentlicher Bedeutung. Visuell wird die Fourier-Transformation durch ein Diagramm dargestellt, das die Amplitude und Frequenz jeder Sinuskurve angibt. Die folgende Gleichung stellt die zeitkontinuierliche Fourier-Transformation dar. Die Gleichung erfasst, wie jedes zeitkontinuierliche Signal als Summe (Integral) von Sinuskurven aller möglichen Frequenzen dargestellt werden kann:
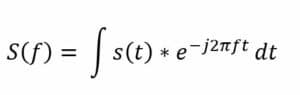
Dabei ist:
Die Fast-Fourier-Transformation (FFT) kann sowohl in Echtzeit- als auch in Nachbearbeitungskontexten angewendet werden. Die Unterscheidung zwischen beiden hängt in erster Linie von der Anwendung und den spezifischen Anforderungen der jeweiligen Aufgabe ab.
Echtzeit-FFT:
Nachbearbeitungs-FFT:
Bei der Messung der FFT (Fast Fourier Transform) wird ein Zeitbereichssignal erfasst und anschließend in den Frequenzbereich transformiert, um seine Frequenzkomponenten zu analysieren. Hier ist eine grundlegende Schritt-für-Schritt-Anleitung zur Messung der FFT:
Zur Messung der FFT können Sie verschiedene Geräte und Software verwenden:
Ein FFT-Analysator oder Fast-Fourier-Transformations-Analysator ist ein Gerät, das eine Frequenzanalyse von Signalen ermöglicht und häufig in Audio-, Vibrationsstudien und verschiedenen anderen Anwendungen verwendet wird. Es nutzt den FFT-Algorithmus, um ein Signal aus seinem ursprünglichen Zeitbereich in den Frequenzbereich umzuwandeln. Hier finden Sie eine detailliertere Aufschlüsselung der Funktionen eines FFT-Analysators:
Spectral Leakage ist ein Phänomen, das die Ergebnisse einer FFT-Analyse verfälschen kann. Bei der Durchführung einer FFT wird grundsätzlich davon ausgegangen, dass sich das Signal in der Zeitaufzeichnung auf unbestimmte Zeit wiederholt. Diese Annahme wird jedoch verletzt, wenn die Anzahl der Zyklen des Signals in diesem Datensatz keine ganze Zahl (nicht ganzzahlig) ist. Diese Diskrepanz zwischen der angenommenen Wiederholung und dem tatsächlichen Signal kann zu spektralen Lecks führen. Durch spektrale Leckage kann die Energie einer bestimmten Frequenz über benachbarte Frequenzlinien oder -bereiche verteilt werden, wodurch das Ergebnis weniger genau wird.
Sowohl Anti-Aliasing als auch die Nyquist-Frequenz sind entscheidende Konzepte, die es bei der Signalabtastung und der Durchführung von FFT-Analysen (Fast Fourier Transform) zu verstehen gilt:
Beim Abtasten eines kontinuierlichen Signals, um ein diskretes Signal für die digitale Verarbeitung (wie FFT) zu erhalten, besagt das Nyquist-Theorem (oder Shannon-Nyquist-Abtasttheorem), dass die Abtastfrequenz mindestens doppelt so hoch sein muss wie die höchste im Signal vorhandene Frequenz, um dies zu ermöglichen das ursprüngliche kontinuierliche Signal vollständig darstellen und später ohne Informationsverlust rekonstruieren. Die höchste zulässige Frequenz im Signal, die der Hälfte der Abtastrate entspricht, ist die Nyquist-Frequenz. Wenn fS die Abtastfrequenz ist, beträgt die Nyquist-Frequenz fN mathematisch: fN=fS/2
Um Aliasing zu verhindern, wird ein Anti-Aliasing-Filter eingesetzt. Bei diesem Filter handelt es sich um einen analogen Tiefpassfilter, der vor der Abtastung auf das Signal angewendet wird. Sein Zweck besteht darin, Frequenzen im Signal zu dämpfen oder zu eliminieren, die höher als die Nyquist-Frequenz sind, um so sicherzustellen, dass die abgetastete Version des Signals keine irreführenden Frequenzinformationen enthält. Dadurch wird sichergestellt, dass die diskrete Version des Signals eine echte Darstellung des kontinuierlichen Signals bis zur Nyquist-Frequenz ist.
Im Zusammenhang mit FFT: Wenn bei der Durchführung einer FFT an abgetasteten Daten die Daten nicht korrekt abgetastet wurden (d. h. mit einer ausreichend hohen Rate) oder wenn kein geeigneter Anti-Aliasing-Filter angewendet wurde, kann das resultierende Frequenzspektrum fehlerhaft sein Alias-Frequenzen enthalten. Dies kann zu falschen oder irreführenden Interpretationen des Frequenzinhalts des Signals führen.
Die Mittelung im Rahmen der FFT wird verwendet, um das Signal-Rausch-Verhältnis zu verbessern und eine genauere Darstellung des Spektrums zu ermöglichen, insbesondere bei der Analyse nichtperiodischer Signale wie Rauschen oder Musik.
Die auf Audio angewendete FFT (Fast Fourier Transform) bezieht sich auf den Prozess der Umwandlung eines Audiosignals vom Zeitbereich in den Frequenzbereich. Diese Transformation ermöglicht es uns, die verschiedenen Frequenzkomponenten (Bässe, Mitten, Höhen usw.) zu sehen, die zu einem bestimmten Zeitpunkt in einem Audiosignal vorhanden sind. Wenn Sie beispielsweise ein Musikstück analysieren, zerlegt eine FFT das Signal, um zu zeigen, wie viel Energie bei jeder Frequenz vorhanden ist. Dadurch könnten gleichzeitig der niederfrequente Schlag einer Bassdrum, die mittelfrequenten Töne einer Gitarre und das hochfrequente Zischen eines Beckens zum Vorschein kommen.
Ein FFT-Audioanalysator ist ein Werkzeug oder Gerät, das die FFT auf Audiosignale anwendet und es Benutzern ermöglicht, den Frequenzinhalt des Signals zu visualisieren. Diese Visualisierung erfolgt häufig in Form eines Spektrums, wobei die x-Achse die Frequenz (von niedrig nach hoch) und die y-Achse die Amplitude darstellt (häufig in einer logarithmischen Skala wie dB). FFT-Audioanalysatoren werden in einer Reihe von Anwendungen eingesetzt:
Als menschlicher Hörbereich wird allgemein angenommen, dass er zwischen 20 Hz und 20.000 Hz (oder 20 kHz) liegt. Wenn also ein FFT-Audioanalysator zur Analyse von Audiosignalen verwendet wird, die für den menschlichen Gebrauch bestimmt sind (wie Musik oder Sprache), konzentriert sich das Frequenzspektrum typischerweise auf diesen Bereich. Es ist erwähnenswert, dass wir zwar in diesem Bereich hören können, unsere Empfindlichkeit gegenüber Frequenzen jedoch nicht einheitlich ist. Der Mensch reagiert am empfindlichsten auf Frequenzen zwischen 2 kHz und 4 kHz und weniger empfindlich auf sehr niedrige und sehr hohe Frequenzen. Ein FFT-Audioanalysator stellt alle Frequenzen basierend auf ihrer tatsächlichen Energie im Signal dar und nicht darauf, wie Menschen sie wahrnehmen.
Die Verwendung von Fenstern ist bei der Durchführung von FFT-basierten Messungen von entscheidender Bedeutung. Fenstern hilft dabei, bestimmte Probleme zu mildern, die mit der Art der FFT und den Eigenschaften der zu analysierenden Signale verbunden sind. Eine Fensterfunktion ist eine mathematische Funktion, die auf das Signal angewendet wird, um die Auswirkungen von Spektralverlusten abzuschwächen. Verschiedene Fenster haben unterschiedliche Eigenschaften und die Wahl des Fensters beeinflusst das Ergebnis der FFT-Analyse. Der Text erwähnt drei spezifische Arten von Fenstern:
Unterschiedliche Fenster eignen sich für unterschiedliche Szenarien.
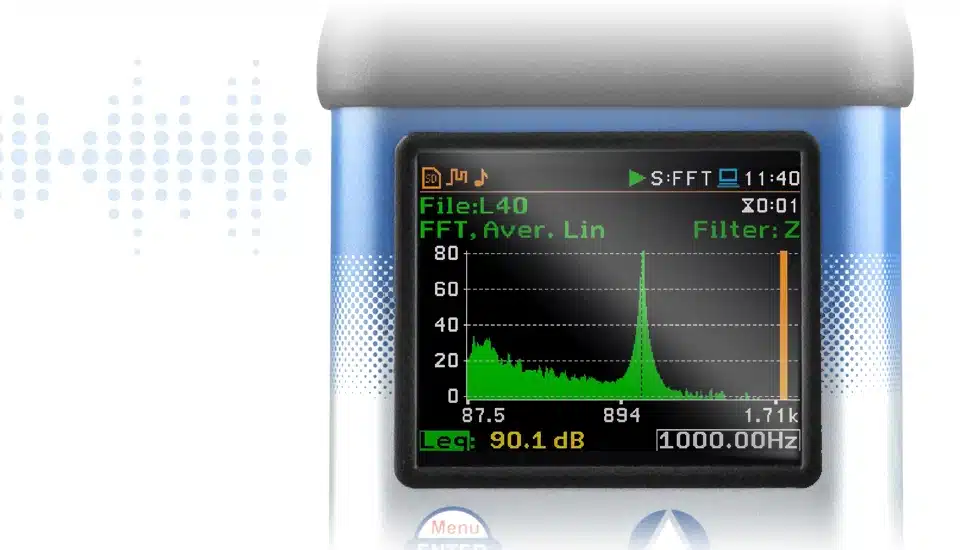
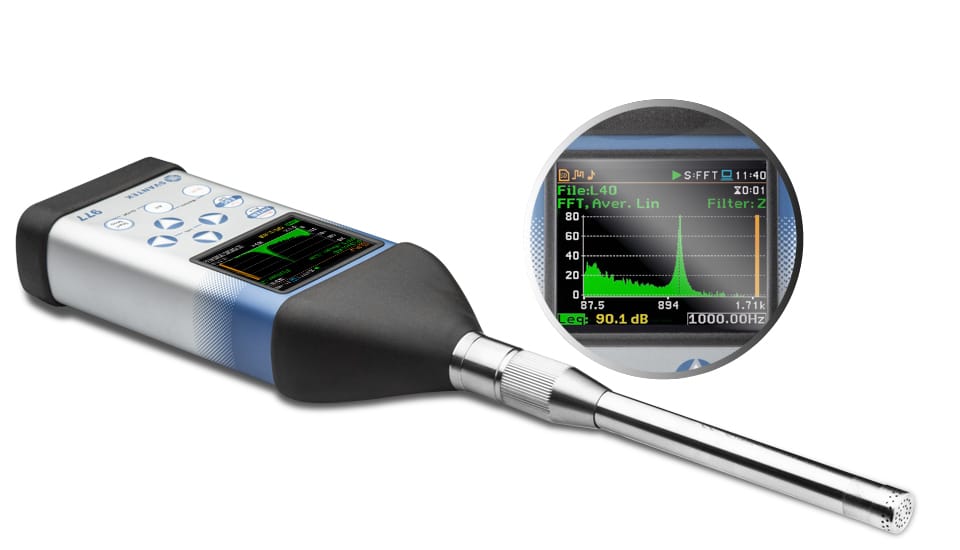
FFT in Svantek-Messgeräten ermöglicht es Benutzern, die Frequenzkomponenten von Schall oder Vibrationen zu verstehen, die sie messen. Dies ist für verschiedene Anwendungen von entscheidender Bedeutung, darunter Geräusch- und Vibrationsbewertungen, Fehlerbehebung und mehr. Bei Svantek-Instrumenten ist FFT (Fast Fourier Transform) ein Rechenalgorithmus, der ein Signal aus seinem ursprünglichen Bereich (Zeitbereich) in seine Teilfrequenzen umwandelt. Es bietet eine Möglichkeit, die unterschiedlichen Frequenzkomponenten von Signalen zu analysieren und ermöglicht detaillierte Einblicke in die Eigenschaften von Schall- oder Vibrationsmessungen. Die FFT-Funktionalität in Svantek-Instrumenten arbeitet mit ihrem Pegelmesser zusammen und kann Ergebnisse als Spektren in einer speziellen Spektrumansicht anzeigen.
Die FFT-Fähigkeiten von Svantek sind sowohl auf die Akustik- als auch auf die Vibrationsanalyse ausgerichtet, sodass sich die Instrumente für eine Vielzahl von Anwendungen eignen, von Umgebungslärmstudien bis hin zur Überwachung industrieller Maschinen:
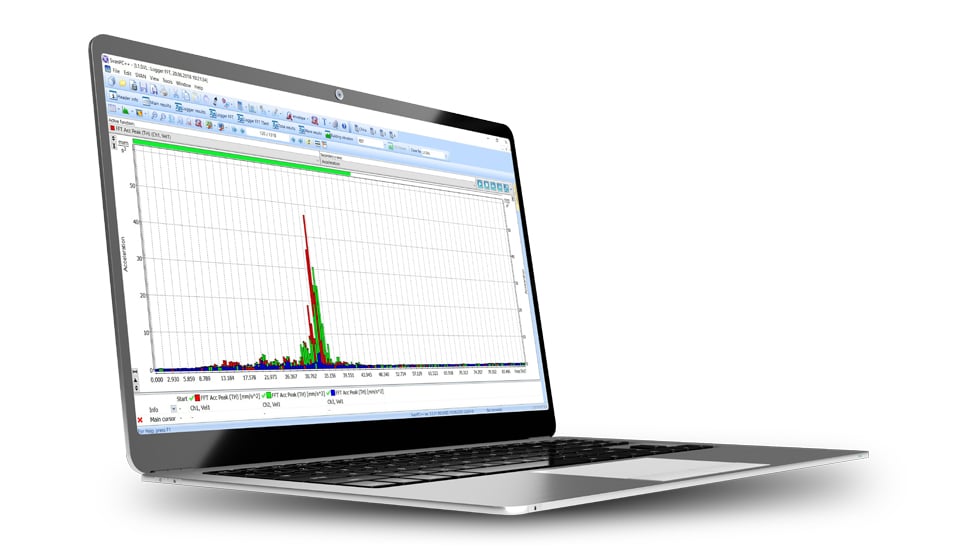
Das FFT-Verfahren bei Gebäudeerschütterungen ist in der deutschen Norm DIN 4150-3 beschrieben. Die Methode erfordert die Durchführung einer FFT-Analyse für die Peak Particle Velocity (PPV/VMAX), sodass die Mitte eines FFT-Fensters genau auf dem PPV platziert wird. Das Ergebnis einer solchen Analyse ist der PPV-Wert (VMAX) und die entsprechende Dominanzfrequenz (DF) für jede Achse (X, Y, Z). Jedes PPV-Paar und sein DF werden als Punktkoordinaten verwendet, die mit der Grenzkurve verglichen werden.
Zusammenfassung
Schnelle FFT-Fourier-Transformation: Wichtige Erkenntnisse:
Ein autorisierter SVANTEK-Berater hilft Ihnen mit Details wie dem erforderlichen Zubehör für Ihre Lärm- und Vibrationsüberwachungsaufgabe.
