Transformée de Fourier rapide FFT
La transformée de Fourier rapide FFT permet la décomposition des signaux en leurs sinusoïdes constitutives, permettant une analyse dans le domaine fréquentiel.
La transformée de Fourier rapide FFT permet la décomposition des signaux en leurs sinusoïdes constitutives, permettant une analyse dans le domaine fréquentiel.
La transformée de Fourier rapide FFT est un algorithme utilisé pour calculer plus efficacement la transformée de Fourier discrète (TFD) et son inverse. La DFT est une transformation utilisée dans le traitement du signal et le traitement d’images, entre autres domaines, pour transformer un signal discret en sa représentation dans le domaine fréquentiel. La FFT accélère le processus de calcul de la DFT, lui permettant d’être utilisée dans des applications en temps réel et pour de grands ensembles de données.
La FFT a été co-découverte par James W. Cooley et John W. Tukey en 1965. Bien que l’algorithme ait certainement constitué une avancée majeure, il convient de noter que bon nombre de ses idées fondamentales existaient depuis un certain temps, mais les travaux de Cooley et Tukey ont apporté il prend de l’importance à l’ère numérique, en particulier avec l’essor de l’informatique numérique. Leur version de l’algorithme a considérablement réduit la complexité informatique liée au traitement de grands ensembles de données, rendant le traitement du signal numérique plus réalisable et plus efficace.
La FFT est un algorithme optimisé conçu pour calculer rapidement la transformée de Fourier discrète (TFD) et son inverse. L’avantage de la FFT réside dans son efficacité. Alors qu’un calcul direct de la DFT nécessite des opérations O(N^2) (temps quadratique), l’algorithme FFT permet le même calcul en opérations O(N log N), ce qui constitue une accélération significative pour les grands ensembles de données.
L’algorithme FFT (Fast Fourier Transform) est utilisé dans un large éventail d’applications car il peut convertir un signal de son domaine temporel à son domaine fréquentiel, et vice versa. Comprendre les composantes fréquentielles d’un signal peut fournir des informations précieuses sur la nature, le comportement et les propriétés de ce signal.
Qu'est-ce que l'équation FFT ?
La FFT est un algorithme qui calcule efficacement la DFT, donc l’équation est la même que l’équation DFT. Cependant, il convient de noter qu’il existe de nombreux algorithmes FFT différents (par exemple, base-2, base divisée, etc.), et chacun a ses propres étapes et subtilités spécifiques.
Qu'est-ce que le TFD ?
La transformée de Fourier discrète DFT est un outil mathématique puissant utilisé pour transformer des signaux discrets et périodiques de leur représentation dans le domaine temporel en une représentation dans le domaine fréquentiel. Cela permet l’analyse et la manipulation dans le domaine fréquentiel avant de potentiellement revenir au domaine temporel avec la DFT inverse. La DFT, que la FFT calcule efficacement, est définie pour une séquence x[n] de longueur N comme :
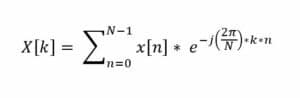
Où:
e est la base du logarithme népérien (approximativement égale à 2,71828).
Il existe de nombreuses applications FFT :
L’utilisation de la FFT présente de nombreux avantages dans diverses applications :
La transformée de Fourier est un concept mathématique plus large utilisé pour transformer les signaux entre les domaines temporel (ou spatial) et fréquentiel. La transformée de Fourier rapide est un algorithme spécifique et optimisé pour calculer plus rapidement la DFT, qui est la version échantillonnée de FT.
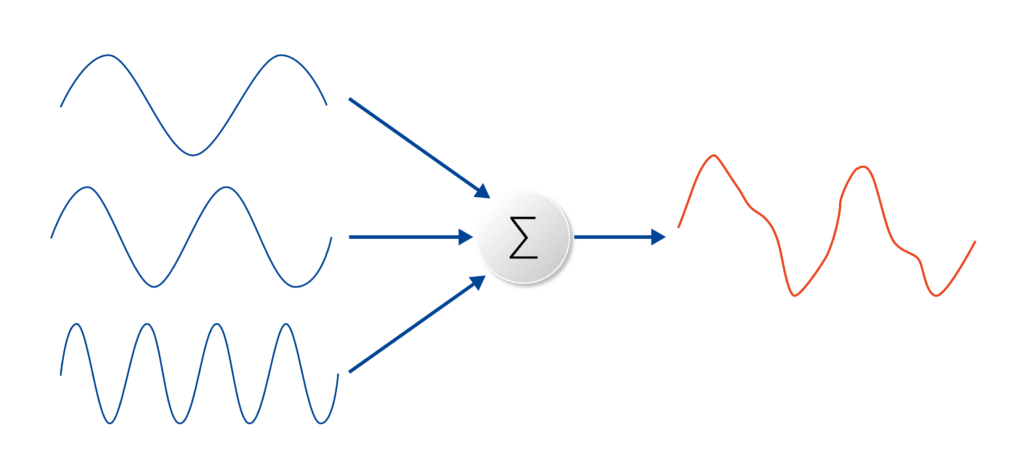
La transformée de Fourier décompose une forme d’onde en une somme de sinusoïdes de fréquences différentes. Cela signifie que la transformée de Fourier représente les mêmes informations que la forme d’onde originale, uniquement dans le domaine fréquentiel (par opposition au domaine temporel). La méthodologie de l’analyse par transformée de Fourier est essentielle pour résoudre efficacement des problèmes dans de nombreux contextes techniques et scientifiques. Visuellement, la transformée de Fourier est représentée par un diagramme indiquant l’amplitude et la fréquence de chaque sinusoïde. L’équation ci-dessous représente la transformée de Fourier en temps continu. L’équation montre comment tout signal en temps continu peut être représenté comme une somme (intégrale) de sinusoïdes de toutes les fréquences possibles :
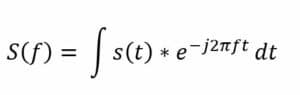
Où:
La transformée de Fourier rapide (FFT) peut être appliquée à la fois dans des contextes en temps réel et en post-traitement. La distinction entre les deux dépend principalement de l’application et des exigences spécifiques de la tâche à accomplir.
FFT en temps réel :
FFT de post-traitement :
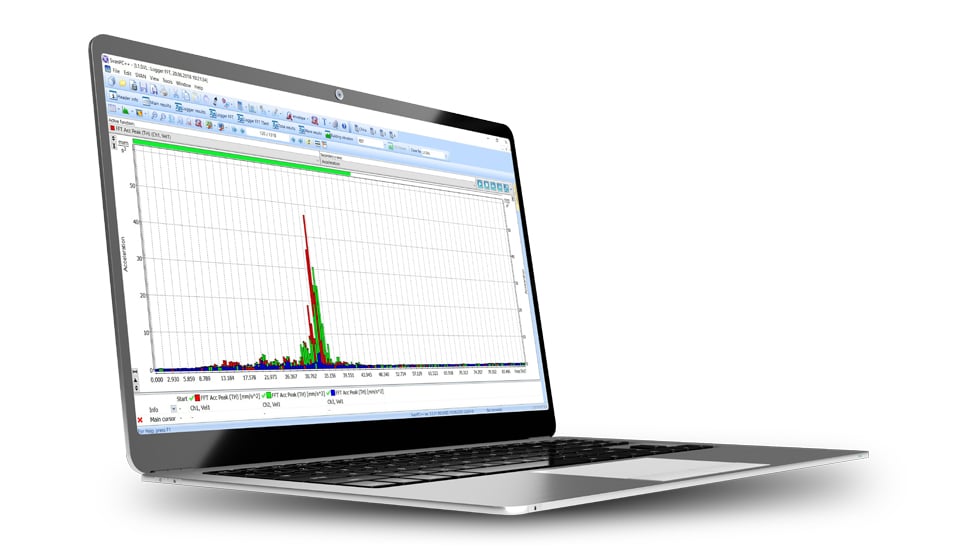
Mesurer la FFT (Fast Fourier Transform) consiste à capturer un signal dans le domaine temporel puis à le transformer dans le domaine fréquentiel pour analyser ses composantes fréquentielles. Voici un guide de base étape par étape sur la façon de mesurer la FFT :
Pour mesurer la FFT, vous pouvez utiliser divers équipements et outils :
Un analyseur FFT, ou analyseur de transformation de Fourier rapide, est un appareil qui fournit une analyse de fréquence des signaux, couramment utilisé dans les études audio, vibratoires et diverses autres applications. Il utilise l’algorithme FFT pour transformer un signal de son domaine temporel d’origine vers le domaine fréquentiel. Voici une description plus détaillée de ce que fait un analyseur FFT :
La fuite spectrale est un phénomène qui peut fausser les résultats d’une analyse FFT. Lors de l’exécution d’une FFT, il existe une hypothèse inhérente selon laquelle le signal dans l’enregistrement temporel se répète indéfiniment. Cependant, cette hypothèse n’est pas respectée si le nombre de cycles du signal dans cet enregistrement n’est pas un nombre entier (non intégral). Cet écart entre la répétition supposée et le signal réel peut conduire à une fuite spectrale. Les fuites spectrales peuvent répartir l’énergie d’une fréquence spécifique sur des lignes ou des compartiments de fréquences adjacents, rendant le résultat moins précis.
L’anticrénelage et la fréquence de Nyquist sont des concepts cruciaux à comprendre lors de l’échantillonnage de signaux et de l’exécution d’analyses FFT (Fast Fourier Transform) :
Lors de l’échantillonnage d’un signal continu pour obtenir un signal discret pour un traitement numérique (comme la FFT), le théorème de Nyquist (ou théorème d’échantillonnage de Shannon-Nyquist) stipule que la fréquence d’échantillonnage doit être au moins deux fois la fréquence la plus élevée présente dans le signal pour pouvoir représenter entièrement et reconstruire plus tard le signal continu d’origine sans aucune perte d’informations. La fréquence la plus élevée autorisée dans le signal, qui correspond à la moitié du taux d’échantillonnage, est la fréquence de Nyquist. Mathématiquement, si fS est la fréquence d’échantillonnage, la fréquence de Nyquist fN est : fN=fS/2
Pour éviter le crénelage, un filtre anti-crénelage est utilisé. Ce filtre est un filtre passe-bas analogique appliqué au signal avant l’échantillonnage. Son objectif est d’atténuer ou d’éliminer les fréquences du signal supérieures à la fréquence de Nyquist, garantissant ainsi que la version échantillonnée du signal ne contient pas d’informations de fréquence trompeuses. Ce faisant, il garantit que la version discrète du signal est une véritable représentation du signal continu jusqu’à la fréquence de Nyquist.
Dans le contexte de la FFT : lors de l’exécution d’une FFT sur des données échantillonnées, si les données n’ont pas été échantillonnées correctement (c’est-à-dire à un débit suffisamment élevé) ou si un filtre anti-aliasing approprié n’a pas été appliqué, le spectre de fréquences résultant peut contiennent des fréquences crénelées. Cela peut conduire à des interprétations incorrectes ou trompeuses du contenu fréquentiel du signal.
La moyenne dans le contexte de la FFT est utilisée pour améliorer le rapport signal/bruit et fournir une représentation plus précise du spectre, en particulier lors de l’analyse de signaux non périodiques comme le bruit ou la musique.
La FFT (Fast Fourier Transform) appliquée à l’audio fait référence au processus de conversion d’un signal audio du domaine temporel vers le domaine fréquentiel. Cette transformation nous permet de voir les différentes composantes fréquentielles (graves, médiums, aigus, etc.) présentes dans un signal audio à un instant donné. Par exemple, lors de l’analyse d’un morceau de musique, une FFT décompose le signal pour montrer la quantité d’énergie présente à chaque fréquence. Cela pourrait révéler à la fois le bruit sourd d’une grosse caisse, les sons de moyenne fréquence d’une guitare et le grésillement de haute fréquence d’une cymbale.
Un analyseur audio FFT est un outil ou un appareil qui applique la FFT aux signaux audio, permettant aux utilisateurs de visualiser le contenu fréquentiel du signal. Cette visualisation se présente souvent sous la forme d’un spectre, où l’axe des x représente la fréquence (de faible à élevée) et l’axe des y représente l’amplitude (souvent sur une échelle logarithmique comme dB). Les analyseurs audio FFT sont utilisés dans une gamme d’applications :
La plage auditive humaine est généralement considérée comme allant de 20 Hz à 20 000 Hz (ou 20 kHz). Ainsi, lorsqu’un analyseur audio FFT est utilisé pour analyser des signaux audio destinés à la consommation humaine (comme la musique ou la parole), le spectre de fréquences se concentre généralement sur cette plage. Il convient de noter que même si nous pouvons entendre dans cette plage, notre sensibilité aux fréquences n’est pas uniforme. Les humains sont plus sensibles aux fréquences comprises entre 2 kHz et 4 kHz et moins sensibles aux très basses et très hautes fréquences. Un analyseur audio FFT représentera toutes les fréquences en fonction de leur énergie réelle dans le signal, et non de la façon dont les humains les perçoivent.
L’utilisation de fenêtres est cruciale lors de l’exécution de mesures basées sur la FFT. Windows aide à atténuer certains problèmes inhérents à la nature de la FFT et aux propriétés des signaux analysés. Une fonction de fenêtrage est une fonction mathématique appliquée au signal pour atténuer les effets de la fuite spectrale. Différentes fenêtres ont des propriétés différentes et le choix de la fenêtre affecte le résultat de l’analyse FFT. Le texte mentionne trois types spécifiques de fenêtres :
Différentes fenêtres sont adaptées à différents scénarios.
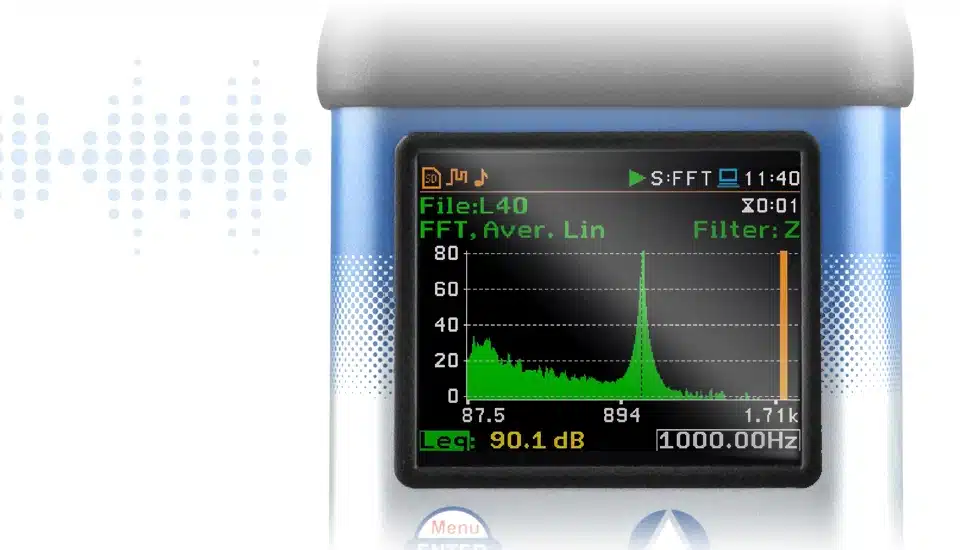
La FFT dans les instruments Svantek permet aux utilisateurs de comprendre les composantes fréquentielles des sons ou des vibrations qu’ils mesurent. Ceci est crucial pour diverses applications, notamment les évaluations du bruit et des vibrations, le dépannage, etc. Dans les instruments Svantek, la FFT (Fast Fourier Transform) est un algorithme de calcul qui transforme un signal de son domaine d’origine (domaine temporel) en ses fréquences constitutives. Il fournit un moyen d’analyser les composantes de fréquence distinctes des signaux, facilitant ainsi un aperçu détaillé des caractéristiques des mesures sonores ou vibratoires. La fonctionnalité FFT des instruments Svantek fonctionne conjointement avec leur indicateur de niveau et peut afficher les résultats sous forme de spectres dans une vue Spectre dédiée.
Les capacités FFT de Svantek sont orientées vers l’analyse acoustique et vibratoire, ce qui rend leurs instruments adaptés à une variété d’applications allant des études de bruit ambiant à la surveillance des machines industrielles :
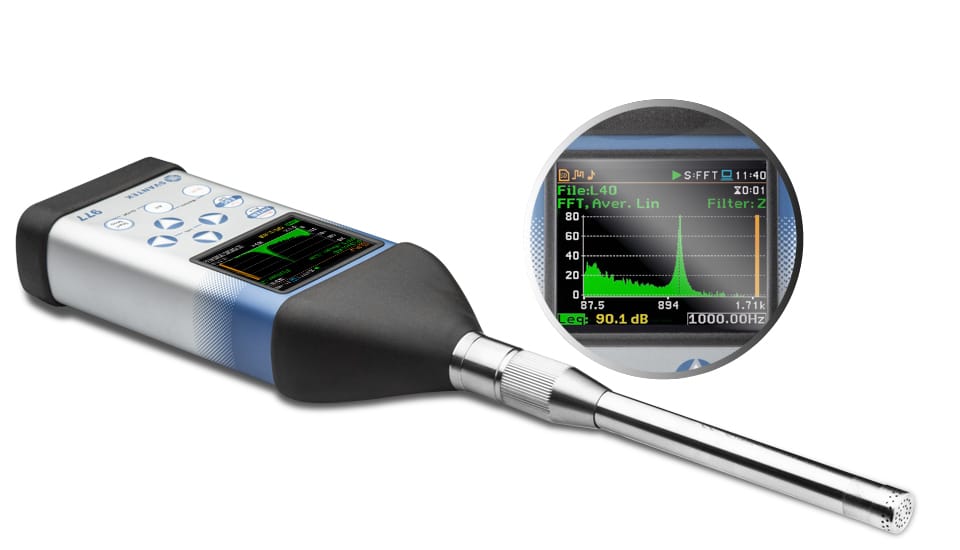
La méthode FFT pour les vibrations des bâtiments est décrite dans la norme allemande DIN 4150-3. La méthode nécessite d’effectuer une analyse FFT pour la vitesse maximale des particules (PPV), de manière à ce que le milieu d’une fenêtre FFT soit placé exactement sur la PPV. Le résultat d’une telle analyse est la valeur PPV et sa fréquence dominante (DF) correspondante pour chaque axe (X, Y, Z). Chaque paire de PPV et son DF sont utilisés comme coordonnées de points qui sont comparées à la courbe limite.
Résumé
Transformée de Fourier rapide FFT : points à retenir :
Un consultant agréé SVANTEK vous aidera avec les détails tels que les accessoires requis pour votre tâche de surveillance du bruit et des vibrations.
