svantek-academie
svantek.com

Définition, caractéristiques et utilisation des ondes sonores en acoustique

Une onde sonore est une perturbation mécanique qui se propage dans un milieu tel que l’air, l’eau ou des solides, transportant de l’énergie et des informations via des oscillations de pression et le déplacement de particules. Il englobe une large gamme de fréquences, y compris celles audibles par l’homme (20 Hz à 20 kHz), ainsi que les infrasons et les ultrasons, et est fondamental pour de nombreuses applications dans les domaines de la communication, de la musique, de l’imagerie médicale et de la surveillance de l’environnement.

Qu'est-ce qu'une onde sonore ?

Une onde sonore, également connue sous le nom d’onde acoustique, est un type d’onde mécanique qui se propage dans un milieu, tel que l’air, l’eau ou des solides, en raison de la vibration d’un objet. Il se caractérise par sa capacité à transporter de l’énergie et des informations à travers le support, se manifestant par des propriétés physiques telles que la fréquence, l’amplitude, la longueur d’onde et la vitesse. Les ondes sonores sont fondamentalement des ondes longitudinales, où le déplacement du milieu est parallèle à la direction de propagation des ondes, conduisant à des régions de compression et de raréfaction.

Le terme « onde de pression acoustique » est souvent utilisé dans un sens large pour désigner les ondes situées dans la plage audible par l’homme, soit environ entre 20 Hz et 20 kHz. En revanche, « onde acoustique » est un terme préféré dans les contextes scientifiques, techniques et techniques, englobant à la fois les ondes sonores et les ondes de pression atmosphérique en dehors de la plage auditive humaine, y compris les infrasons (en dessous de 20 Hz) et les ultrasons (au-dessus de 20 kHz). Cette distinction met en évidence la nature polyvalente des ondes sonores, qui sont non seulement cruciales pour la communication, la musique et l’interaction environnementale, mais jouent également un rôle central dans diverses applications telles que l’imagerie médicale, les diagnostics industriels et la surveillance environnementale.

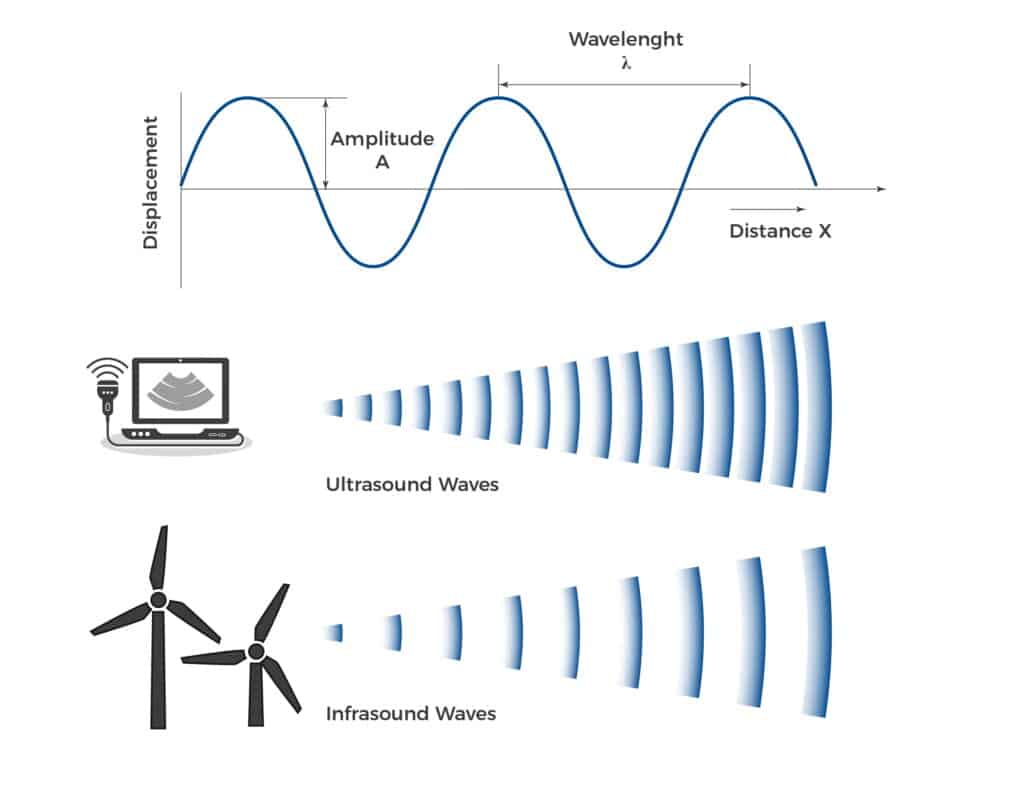
what is sound wave

Quelles sont les propriétés de l’onde acoustique ?

Les propriétés des ondes acoustiques englobent plusieurs caractéristiques clés qui décrivent leur comportement lorsqu’elles se propagent dans un milieu. Ces propriétés définissent non seulement les aspects physiques des ondes sonores, mais influencent également la façon dont elles interagissent avec leur environnement et sont perçues par les humains ou détectées par les instruments. Voici un aperçu détaillé :

  1. Fréquence : nombre d’oscillations ou de cycles qui se produisent dans une onde sonore par seconde, mesuré en Hertz (Hz). La fréquence d’une onde sonore détermine la hauteur du son, les fréquences plus élevées produisant des sons plus aigus et les fréquences plus basses produisant des sons plus graves.
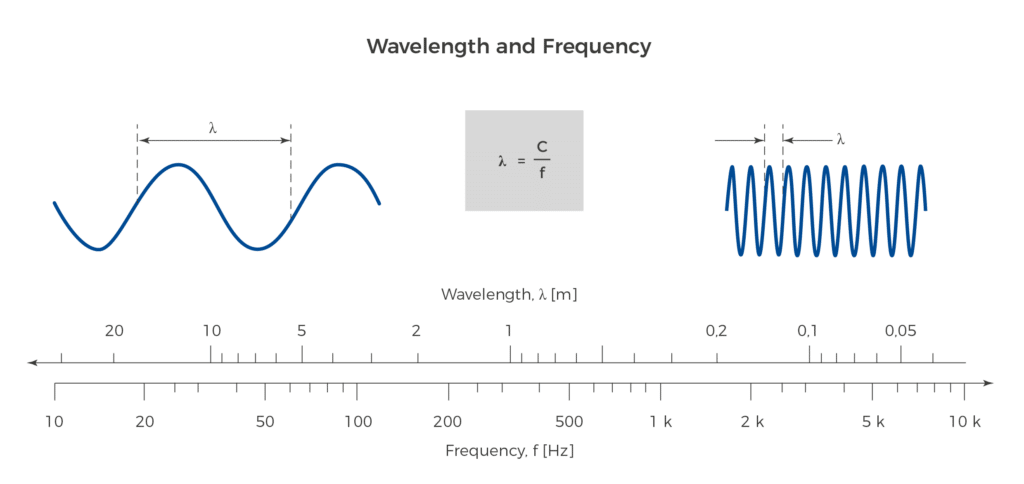
  2. Longueur d’onde : La distance physique entre deux points consécutifs en phase sur une vague, comme une crête à une crête ou un creux à un creux. La longueur d’onde d’une onde sonore (λ) est inversement proportionnelle à la fréquence et directement liée à la vitesse du son (c) et à la fréquence de l’onde (f) par la formule λ=c/f.
  3. L’amplitude d’une onde sonore représente le déplacement maximal des particules par rapport à leur position d’équilibre dû au passage de l’onde. Dans les ondes sonores, l’amplitude est liée à l’intensité ou au volume du son, des amplitudes plus grandes produisant des sons plus forts.
  4. Vitesse : Vitesse à laquelle une onde sonore se propage dans un milieu. La vitesse du son varie en fonction du milieu et de ses propriétés (par exemple, densité, température et élasticité), étant la plus rapide dans les solides, la plus lente dans les liquides et la plus lente dans les gaz.
  5. Intensité : La puissance transportée par une onde sonore par unité de surface, mesurée en watts par mètre carré (W/m2). L’intensité est une mesure de l’énergie de l’onde sonore et est liée à la fois à son amplitude et à sa distance par rapport à la source, influençant le niveau de perception du son.
  6. Phase : décrit la position d’un point dans le temps sur un cycle de forme d’onde. Dans le contexte d’ondes en interaction multiple, les différences de phase peuvent conduire à des phénomènes tels qu’une interférence constructive ou destructrice, affectant de manière significative l’amplitude et l’intensité du son résultant.
acoustic waves
Consultez l'offre d'un sonomètre

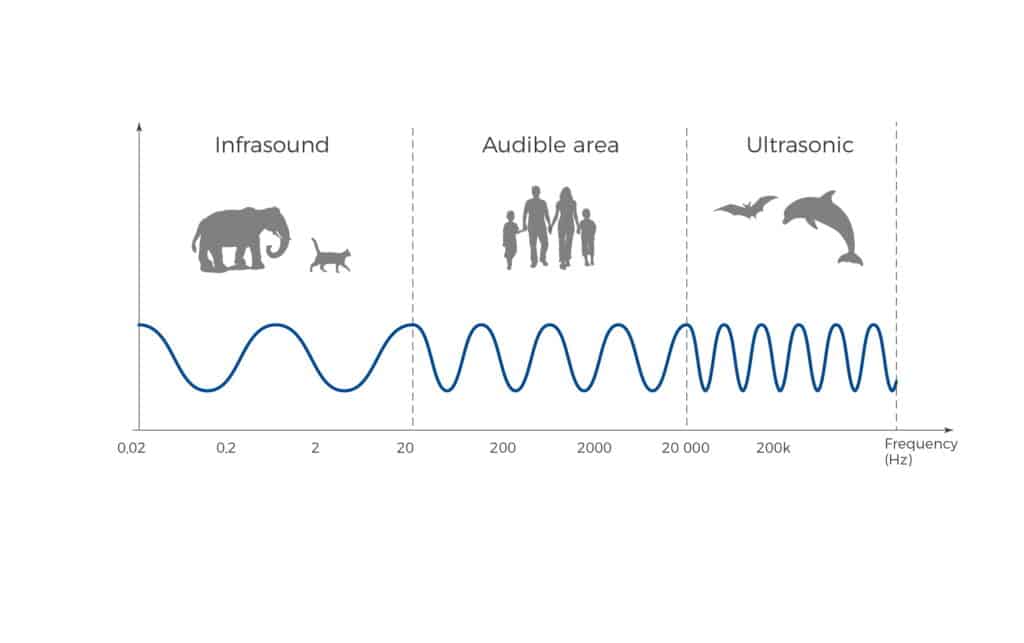
Quels sont les types d’ondes sonores en acoustique ?

Les ondes acoustiques peuvent être classées en fonction de leur mode de propagation, de leur gamme de fréquences et du milieu dans lequel elles se propagent. Voici un aperçu plus approfondi des principaux types :

Types d’ondes basés sur le mode de propagation

  1. Ondes longitudinales : ces ondes présentent des oscillations de particules parallèles à la direction de déplacement de l’onde. Ils sont répandus dans les fluides (gaz et liquides) et peuvent également se propager à travers les solides. Les ondes longitudinales sont caractérisées par une alternance de compressions et de raréfactions du milieu.
  2. Ondes transversales : Dans ces ondes, le mouvement des particules est perpendiculaire à la direction de propagation de l’onde. Les ondes transversales sont exclusives aux milieux solides, où la déformation par cisaillement est supportée. Ils jouent un rôle important dans la compréhension de l’intérieur de la Terre et des propriétés mécaniques des matériaux.
  3. Ondes de surface : se produisant à la frontière entre deux milieux distincts, les ondes de surface combinent des aspects d’ondes longitudinales et transversales. Leur amplitude diminue avec la profondeur dans le milieu et sont essentiels dans des applications telles que la sismologie et les dispositifs à ondes acoustiques de surface (SAW).

Types d’ondes basés sur la fréquence

  1. Ondes sonores audibles : S’inscrivant dans le spectre auditif humain de 20 Hz à 20 kHz, ces ondes englobent les sons de la vie quotidienne, de la parole et de la musique aux sons environnementaux.
  2. Ondes infrasonores: Avec des fréquences inférieures à 20 Hz, les ondes infrasonores sont imperceptibles pour les humains mais peuvent se propager sur de longues distances et à travers divers milieux. Ils sont utilisés pour étudier les phénomènes naturels et surveiller les conditions environnementales.
  3. Ondes ultrasonores: les fréquences supérieures à 20 kHz, au-delà de l’audition humaine, sont utilisées dans de nombreuses applications, du diagnostic médical (par exemple, l’échographie) au nettoyage industriel et aux tests de matériaux.
What are the types of sound waves in acoustics

Que sont les ondes stationnaires en acoustique ?

Les ondes stationnaires sont un phénomène unique résultant de l’interférence de deux ondes se propageant dans des directions opposées avec la même fréquence. Ils sont caractérisés par des nœuds (points de non-mouvement) et des ventres (points d’oscillation maximale). Les ondes stationnaires sont fondamentales dans l’étude des instruments de musique, de l’acoustique architecturale et dans la conception de cavités résonantes pour diverses applications. Comprendre comment se forment les ondes stationnaires et leurs propriétés contribue au contrôle et à la manipulation précis du son dans les espaces et les appareils.

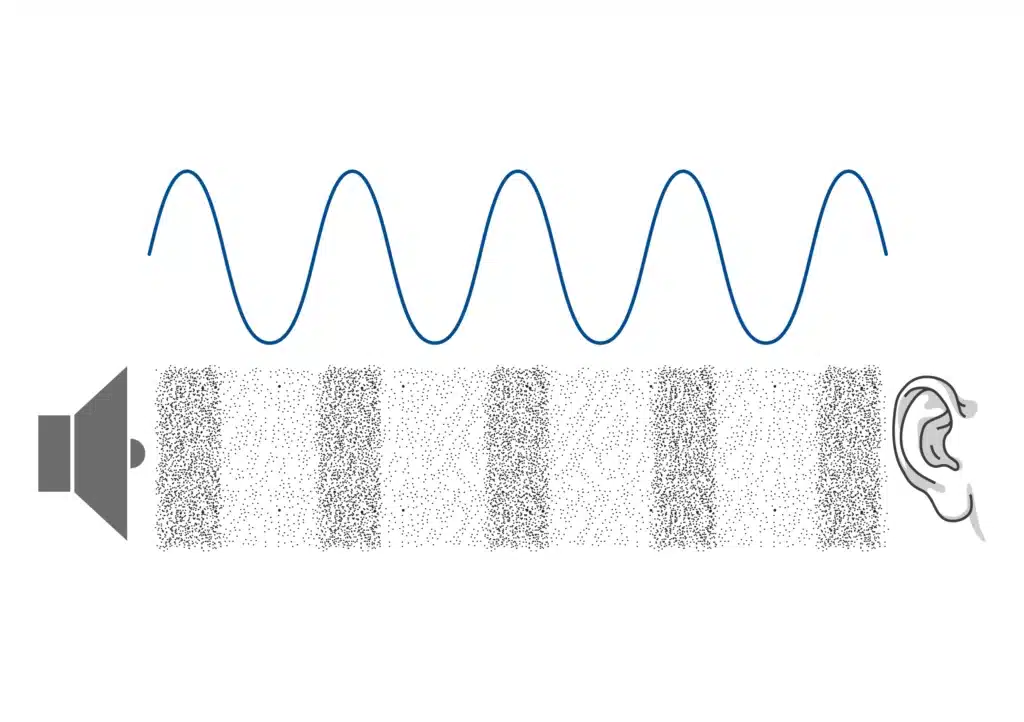
how the wave transfers the sound energy

Comment la vague transfère l’énergie sonore ?

Le transfert d’énergie sonore par une onde est lié au mouvement des particules et au passage de l’énergie à travers le milieu.

Dans une onde sonore, les particules du milieu (telles que les molécules d’air) se déplacent d’avant en arrière dans une direction parallèle à la direction de propagation de l’onde (semblable à un diapason), mais elles ne voyagent pas elles-mêmes avec l’onde sur de longues distances. . Au lieu de cela, c’est l’énergie transportée par la vague qui avance à travers le milieu.

Ce mouvement de va-et-vient des particules entraîne des compressions (zones où les particules sont plus rapprochées) et des raréfactions (zones où les particules sont plus éloignées les unes des autres), qui se propagent dans le milieu au fur et à mesure du déplacement de l’onde sonore. Les particules oscillent autour de leurs positions d’équilibre – elles reviennent à leur point de départ une fois l’onde passée.

Le transfert d’énergie s’effectue de la manière suivante :

  1. Initiation : L’onde sonore est initiée par une source vibrante (comme un haut-parleur ou une corde de guitare pincée), qui rapproche les particules du milieu (compression) ou les écarte davantage (raréfaction).
  2. Transmission : Lorsqu’une particule est déplacée de sa position d’équilibre, elle exerce une force sur ses particules voisines en raison de la différence de pression, les faisant également se déplacer. Ce processus se répète de particule en particule, transmettant l’énergie sonore à travers le milieu.
  3. Propagation : Bien que les particules individuelles ne se déplacent que sur une petite distance, l’énergie de l’onde sonore est transmise de particule en particule, permettant à l’onde de se propager à travers le milieu et de transporter l’énergie sonore sur des distances importantes.
  4. Réception : Lorsque l’onde sonore atteint un auditeur (ou un appareil de mesure), les changements de pression oscillants font vibrer le tympan de l’auditeur (ou le diaphragme de l’appareil), permettant au son d’être entendu ou mesuré.

Ce transfert efficace d’énergie, de particule à particule, sans le mouvement global du médium lui-même, est ce qui nous permet d’entendre des sons provenant de sources éloignées, car l’énergie de la source sonore est transmise à travers le médium pour atteindre l’auditeur.

wave transfers the sound energy

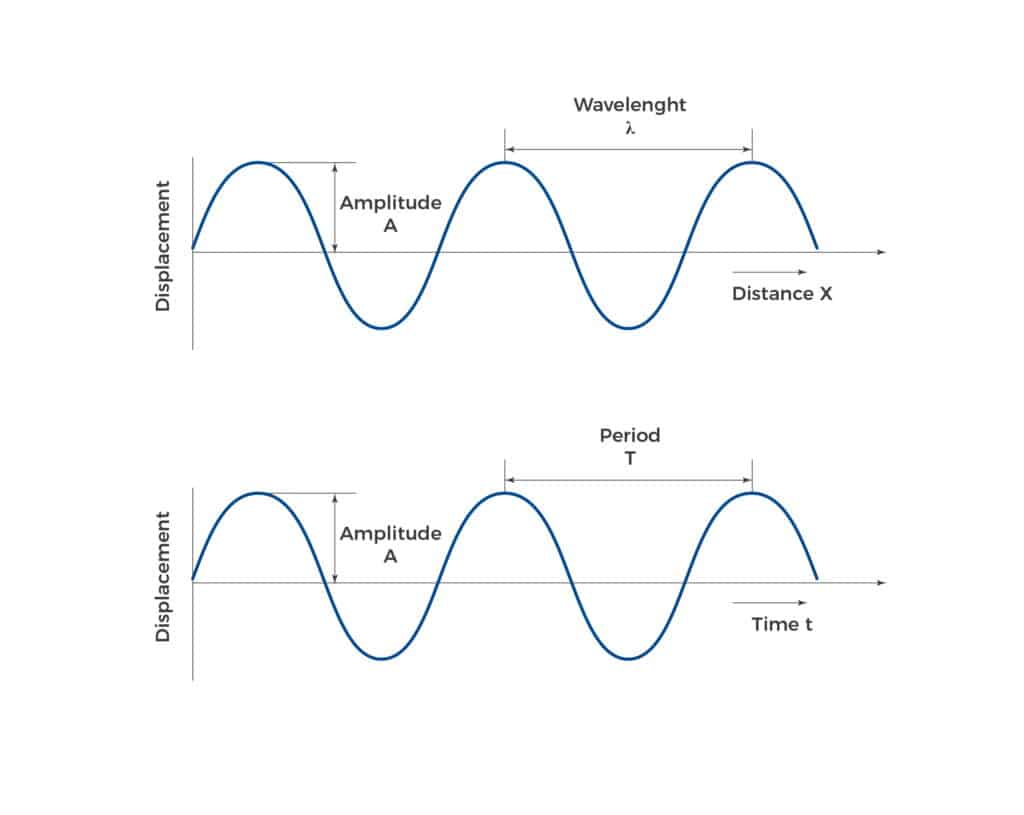
Comment l’onde sonore est-elle visualisée ?

En nous concentrant sur la représentation graphique des ondes sonores, nous utilisons la fonction sinusoïdale pour illustrer la nature oscillatoire de ces ondes, capturant l’essence de la propagation du son à travers différents médiums. Dans ce contexte, les passages par zéro de l’onde sinusoïdale représentent graphiquement les moments où le niveau de pression acoustique est égal à la pression ambiante, indiquant un changement dans la direction du mouvement des particules dans le milieu. Ces croisements sont essentiels pour comprendre la phase de la vague et son interaction avec l’environnement ou d’autres vagues.

La période de l’onde, représentée visuellement par la distance entre les pics ou les creux consécutifs sur le graphique, est directement corrélée à la fréquence de l’onde sonore. La fréquence, mesurée en Hertz (Hz), désigne le nombre d’oscillations par seconde et est inversement liée à la période ; des fréquences plus élevées correspondent à des périodes plus courtes et vice versa. Cette relation est fondamentale en acoustique, car elle dicte la hauteur du son perçu par l’oreille humaine.

L’amplitude, une autre propriété critique des ondes sonores, reflète l’étendue maximale d’une vibration ou d’une oscillation par rapport à la position d’équilibre, qui peut être mesurée en Pascals (Pa) pour une représentation linéaire ou en décibels (dB) pour une échelle logarithmique. L’amplitude est indicative de l’intensité du son ; des amplitudes plus élevées entraînent des sons plus forts. En termes graphiques, l’amplitude est représentée par la hauteur des pics d’onde à partir de l’axe central (ligne zéro) sur le graphique sinusoïdal.

Les ondes sonores complexes, généralement rencontrées dans des scénarios du monde réel, peuvent être décomposées en ondes sinusoïdales plus simples grâce à un processus appelé analyse de Fourier. Cette décomposition permet d’extraire les fréquences fondamentales et leurs harmoniques, facilitant une compréhension plus approfondie des caractéristiques du son et permettant un post-traitement efficace en acoustique. Cette approche analytique souligne l’importance des représentations d’ondes sinusoïdales dans la visualisation et l’interprétation de la nature complexe des ondes sonores.

Comment les ondes sonores sont utilisées en acoustique ?

En acoustique, les ondes sonores sont souvent largement utilisées pour analyser et améliorer les caractéristiques acoustiques des environnements, des salles de concert et studios d’enregistrement aux espaces publics et zones résidentielles. Ce processus implique souvent l’utilisation de générateurs de sons et de sonomètres comme outils clés pour mesurer les propriétés acoustiques et mettre en œuvre les ajustements nécessaires pour une qualité sonore optimale.

  • Générateurs de sons : ces appareils produisent des types spécifiques de bruit, tels que le bruit rose ou le bruit blanc, qui ont des caractéristiques spectrales distinctes. Le bruit rose, par exemple, a une énergie égale par octave, ce qui le rend utile pour évaluer la réponse acoustique sur différentes bandes de fréquences. Le bruit blanc, quant à lui, contient une énergie égale à toutes les fréquences, fournissant ainsi un signal de test large et uniforme. En remplissant une pièce de ces sons, les acoustiques peuvent simuler un large éventail de scénarios acoustiques pour tester minutieusement la réponse de la pièce.
  • Mesure et analyse : Une fois que le générateur de son émet le signal de test, un sonomètre enregistre la réponse de la pièce. Cet équipement sophistiqué capture la façon dont les ondes sonores interagissent avec diverses surfaces et objets dans l’espace, y compris les réflexions, l’absorption et la diffusion. En analysant les différences entre le son émis et ce qui est enregistré, les acoustiques peuvent identifier des défauts acoustiques spécifiques tels que des échos, des points morts ou une réverbération excessive.
  • Améliorer l’acoustique de la pièce: Armés de données sur la réponse acoustique de la pièce, les experts peuvent alors prendre des décisions éclairées sur la manière de modifier l’espace pour obtenir les résultats acoustiques souhaités. Cela peut impliquer de modifier la géométrie de la pièce, d’ajouter ou d’ajuster des matériaux insonorisants ou de mettre en place des diffuseurs pour gérer plus efficacement les réflexions sonores. L’objectif est d’adapter l’environnement acoustique à l’utilisation prévue, qu’il s’agisse de performances musicales, de clarté de la parole ou de contrôle du son ambiant.

Grâce à cette approche méthodique consistant à utiliser des générateurs de sons pour créer un environnement acoustique contrôlé et à utiliser des sonomètres pour des mesures et des analyses précises, les acoustiques peuvent améliorer considérablement les caractéristiques acoustiques d’une pièce. Cela garantit que l’espace répond non seulement aux exigences esthétiques et fonctionnelles, mais offre également une expérience auditive qui améliore l’environnement global pour ses occupants.

Comment les ondes sont-elles utilisées en chambre anéchoïque ?

Dans une chambre anéchoïque, les ondes sont utilisées pour créer un environnement contrôlé qui simule les conditions de champ libre, permettant une mesure et une analyse précises du son sans l’influence des réflexions ou du bruit externe. La conception d’une chambre anéchoïque vise à minimiser les réflexions (échos) et à maximiser l’absorption pour garantir que les ondes sonores émanant d’une source ne rebondissent pas sur les murs, le plafond ou le sol. Ceci est réalisé grâce à l’utilisation de matériaux insonorisants qui recouvrent toutes les surfaces internes de la chambre, généralement sous la forme de mousse en forme de coin ou de chicanes fibreuses.

L’utilisation principale des ondes en chambre anéchoïque implique :

  1. Mesures et tests : Les mesures acoustiques d’appareils tels que des haut-parleurs, des microphones et d’autres équipements audio sont effectuées dans des chambres anéchoïques. L’absence de réflexions garantit que les mesures capturent uniquement le son direct de la source, fournissant ainsi une évaluation claire et incolore de sa sortie acoustique.
  2. Recherche et développement : Les ingénieurs et les chercheurs utilisent des chambres anéchoïques pour étudier les propriétés des ondes sonores et leur interaction avec divers matériaux. Cet environnement contrôlé est idéal pour développer de nouvelles technologies audio, des matériaux aux propriétés acoustiques spécifiques et des techniques de réduction du bruit.
  3. Caractérisation du son : en éliminant les réflexions, les chambres anéchoïques permettent la caractérisation précise du son émis par les objets, y compris leur réponse en fréquence, leurs modèles de directivité et leurs niveaux d’émission. Ces informations sont cruciales pour la conception de systèmes sonores, d’acoustique architecturale et de solutions de contrôle du bruit.
  4. Génération d’ondes planes : dans les chambres anéchoïques, les haut-parleurs peuvent être utilisés pour générer des ondes planes qui imitent le comportement du son dans un environnement ouvert et illimité. Ces ondes planes sont essentielles pour calibrer et tester les microphones et autres capteurs dans des conditions qui ressemblent étroitement à la propagation du son en champ libre dans le monde réel.

En se concentrant sur l’absorption et en minimisant la réflexion, les chambres anéchoïques utilisent les ondes sonores pour fournir un cadre idéal pour des mesures et des recherches acoustiques précises, permettant ainsi les progrès de la technologie audio et l’étude du comportement sonore dans des conditions de champ libre presque parfaites.

how the waves are used in anechoic chamber

Points clés à retenir

    1. Les ondes sonores, ou ondes acoustiques, sont des ondes mécaniques qui se propagent à travers des milieux (air, eau, solides) en raison des vibrations des objets, caractérisées par la fréquence, l’amplitude, la longueur d’onde et la vitesse. Ces ondes peuvent être longitudinales ou transversales, selon la direction de déplacement des particules par rapport à la propagation des ondes.
    2. Le comportement des ondes sonores est défini par plusieurs propriétés, notamment la fréquence, qui détermine la hauteur ; l’amplitude, liée au volume sonore ; la vitesse, qui varie selon le support ; et l’intensité, indiquant le transfert d’énergie.
    3. Les ondes acoustiques varient en fonction de leur mode de propagation (ondes longitudinales, transversales, de surface) et de leur gamme de fréquences (ondes sonores audibles, infrasons et ultrasons), chacune ayant des caractéristiques et des applications distinctes.
    4. Résultant de l’interférence de deux ondes se propageant dans des directions opposées, les ondes stationnaires sont essentielles à la musique, à l’acoustique architecturale et à la conception de cavités résonantes.
    5. L’énergie sonore est transférée à travers le milieu par l’oscillation des particules, l’énergie avançant tandis que les particules elles-mêmes oscillent uniquement autour de leurs positions d’équilibre.
    6. Les ondes sonores sont généralement visualisées à l’aide de fonctions sinusoïdales, illustrant des aspects clés tels que la fréquence, l’amplitude et la phase. Les ondes complexes peuvent être décomposées en ondes plus simples pour analyse.
    7. Les ondes sonores sont utilisées en acoustique pour analyser et améliorer les caractéristiques acoustiques des environnements. Les techniques consistent à générer des types de bruit spécifiques (comme le bruit rose ou blanc) et à analyser la réponse de la pièce pour optimiser l’acoustique.
    8. Les chambres anéchoïques sont des environnements spécialisés qui simulent des conditions de champ libre pour des mesures et des recherches acoustiques précises, en se concentrant sur la minimisation des réflexions et la maximisation de l’absorption.

Demandez l'offre de prix pour
Sonomètre












    Merci d'indiquer l'objet de votre demande :

    J'accepte par la présente le traitement de mes données personnelles, c'est-à-dire mon nom complet et mon adresse e-mail, par SVANTEK SP. ZOO. dont le siège social est à Varsovie, ul. Strzygłowska 81 dans le but de recevoir des informations marketing sur les produits et services proposés par SVANTEK SP. ZOO. via des moyens de communication électroniques, notamment par courrier électronique, conformément aux dispositions de l'article 10 sec. 1 et 2 de la loi sur la fourniture de services par voie électronique.

    J'accepte par la présente le traitement de mes données personnelles, c'est-à-dire mon nom complet et mon numéro de téléphone, par SVANTEK SP. ZOO. dont le siège social est à Varsovie, ul. Strzygłowska 81 aux fins d'activités de marketing utilisant des équipements terminaux de télécommunications et des automates d'appel au sens de la loi sur les télécommunications.

    J'accepte par la présente de recevoir de SVANTEK SP. ZOO. dont le siège social est à Varsovie, ul. Strzygłowska 81, par voie électronique à l'adresse e-mail que j'ai fournie, la newsletter et les informations marketing sur les produits et services proposés par SVANTEK SP. Z O.O., au sens de la loi sur la fourniture de services par voie électronique.


    Je déclare avoir été informé que mes données peuvent être transférées à des entités qui traitent des données personnelles pour le compte de l'Administrateur, en particulier à des distributeurs - ces entités traitent les données sur la base d'un accord avec l'Administrateur et exclusivement conformément à son instructions. Dans de tels cas, l'Administrateur demande aux tiers de maintenir la confidentialité et la sécurité des informations et vérifie qu'ils prennent les mesures appropriées pour protéger les données personnelles.
    Certaines des entités traitant des données personnelles pour le compte de l'Administrateur sont établies en dehors de l'EEE. Dans le cadre du transfert de vos données hors EEE, l'Administrateur vérifie que ces entités offrent des garanties d'un haut niveau de protection des données personnelles. Ces garanties découlent notamment de l'obligation d'appliquer les clauses contractuelles types adoptées par la Commission (UE). Vous avez le droit de demander une copie des clauses contractuelles types en adressant une demande au Responsable du traitement.
    Je déclare avoir été informé de mon droit de retirer à tout moment mon consentement au traitement de mes données personnelles, d'accéder aux données personnelles fournies, de rectifier, effacer, restreindre le traitement et de m'opposer au traitement de mes données, ainsi que ainsi que le droit de déposer une plainte auprès du Président du Bureau de Protection des Données Personnelles en cas de violation des dispositions du RGPD.

    svantek consultant

    Un consultant agréé SVANTEK vous aidera avec les détails tels que les accessoires requis pour votre tâche de surveillance du bruit et des vibrations.

    processing...